AEs

AE

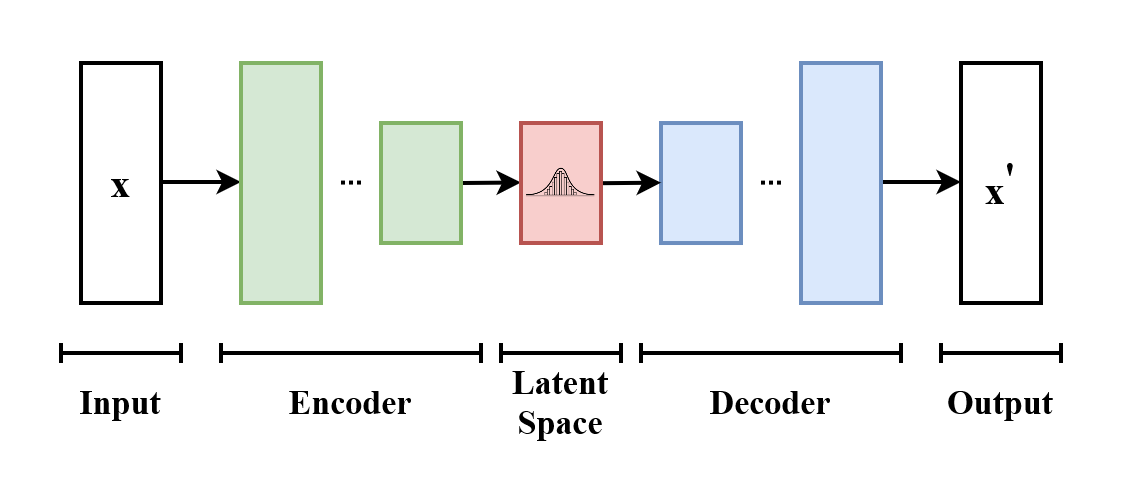
基于 deep learning 的降维算法。

模型由 encoder、decoder 构成，其中 encoder 用于将输入的高维向量编码到低维的 embedding，而 decoder 用于将 embedding 还原到原本的向量空间。

直观上讲，AutoEncoder 之所以能够实现，是因为输入样本的复杂度小于其向量空间维度。一个极端的例子是，对于 $512\times 512$ 的图片，样本空间总共只有两张不同的图片，那么只需要 1 bit 就足以编码该样本空间。

有了这个 embedding，就可以用来做一系列 downstream 的任务。

encoder、decoder的详细结构？

Usage

• Feature Disentanglement：尝试将 embedding 拆分成不同部分，每个部分代表了输入的某一方面特征。例如，对于语音输入，尝试将 embedding 拆分为音色、内容两部分。可以应用到风格迁移中。
• Discrete Representation：尝试用离散值（例如 01 编码、one-hot 编码）来表示 embedding。
• ...... （text as representation、tree as representation）

VAE

该部分内容（尤其是数学推导）主要来自：张振虎的博客 ，其中的内容与Understanding Diffusion Models: A Unified Perspective 的推导类似。

与 AE 的总体架构类似，二者的关键区别在于，AE 编码器输出的 embedding 只是一个张量，而 VAE 则是一个随机变量，该随机变量的均值和方差由编码器给出；同样的，确定 embedding，VAE 解码器输出的也是一个随机变量，其均值由解码器给出，方差为 $I$。记输入为 $x$，输出同样也是 $x$，embedding 为 $z$。

Note

AE 的目标是使得输入输出相同，所以这里使用了相同的符号 $x$ 来表示，但是在推导时需要区分。具体而言，考虑如下情形：

1. 可观测变量 $\mathcal{D}=\{x^1,x^2...x^N\}$：极大似然指的是使得输出变量符合样本，所以这里指的是输出样本，然而对于 AE 而言，样本输入输出相同；
2. $p_{\theta }(x|z)$：指的是输出；
3. $p_{\varphi }(z|x)$：指的是输入。

通过极大似然求解？ 如果通过极大似然法求解，需要极大化观测样本的发生概率。在这里，只有输入 $\mathcal{D}=\{x^1,x^2...x^N\}$ 是可观测的，VAE 的中间 embedding 并不能观测到（其值为何完全由 VAE 决定，不由样本给出）。因此，对数似然函数为：

$$\begin{array}{}\text{(1)}& \ell (\theta ;\mathcal{D})=\sum _{i=1}^N\ln p_{\theta }(x^i)=\sum _{i=1}^N\ln {\int }_z{p}_{\theta }(x^i,z)\end{array}$$

然而，这个式子无法数值求解。

Note

为什么要对隐变量 $z$ 展开？

只看 $p(x)$ 没法进一步展开，而对隐变量 $z$ 展开实际上是结合了 $x$ 生成的实际过程，从而使得接下来的所有推导成为可能。

证据下界（Evidence Lower Bound,ELBO）

expand to see preliminaries

在机器学习领域中，常使用期望的下标来表示随机变量 $x$ 服从分布的概率密度函数：

$$\begin{array}{}& {\mathbb{E}}_{x\sim p(x)}[g(x)]={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}p(x)g(x)\mathrm{d}x={\int }_{x}p(x)g(x)\end{array}$$

Definition

既然无法直接求解 $(\text{1})$，能否找到一个近似表达呢？答案是可以的。首先需要引入一个 $z$ 的概率密度函数 $q_{\varphi }(z)$，其中 $\varphi$ 是未知的参数。然后，可以将$(\text{1})$进行如下化简：

$$\begin{array}{}\text{(2)}& \begin{array}{rl}\ell (\theta ;x)& =\ln p_{\theta }(x)\\ & =\ln {\int }_z{p}_{\theta }(x,z)\text{对隐变量展开}\\ & =\ln {\int }_z{q}_{\varphi }(z)\frac{p_{\theta }(x,z)}{q_{\varphi }(z)}\\ & =\ln {\mathbb{E}}_{q_{\varphi }(z)}\left[\frac{p_{\theta }(x,z)}{q_{\varphi }(z)}\right]\\ & \ge {\mathbb{E}}_{q_{\varphi }(z)}\ln \left[\frac{p_{\theta }(x,z)}{q_{\varphi }(z)}\right]\text{根据Jensen不等式}\\ & ={\int }_z{q}_{\varphi }(z)\ln \left[\frac{p_{\theta }(x,z)}{q_{\varphi }(z)}\right]\\ & =[{\int }_z{q}_{\varphi }(z)\ln p_{\theta }(x,z)-{\int }_z{q}_{\varphi }(z)\ln q_{\varphi }(z)]\\ & \triangleq \mathcal{L}(q,\theta )\end{array}\end{array}$$

由此，可以得出对数似然函数的一个下界 $\mathcal{L}(q,\theta )$，又因为它是证据 $p(x)$ 的下界，因此叫做证据下界。

Derivation Based on $P(x,z)$

对于$(\text{2})$中的 $p(x,z)$ 项，可以作如下分解：

$$\begin{array}{}\text{(3)}& p(x,z)=p(z)p(x|z)=p(x)p(z|x)\end{array}$$

通过两种不同的分解方式，可以分别对 ELBO 进行变换，得出对应的结论。

第一种变换

expand to see preliminaries

KL 散度的定义：

$$\begin{array}{}& KL(P||Q)=\int p(x)\log \frac{p(x)}{q(x)}dx={\mathbb{E}}_{x\sim p(x)}\log \frac{p(x)}{q(x)}\end{array}$$

$$\begin{array}{}\text{(4)}& \begin{array}{rl}\mathcal{L}(q,\theta )& ={\mathbb{E}}_{z\sim q_{\varphi }}[\ln p_{\theta }(x,z)]-{\mathbb{E}}_{z\sim q_{\varphi }}[\ln q_{\varphi }(z)]\\ & ={\mathbb{E}}_{z\sim q_{\varphi }}[\ln p_{\theta }(x)+\ln p_{\theta }(z|x)]-{\mathbb{E}}_{z\sim q_{\varphi }}[\ln q_{\varphi }(z)]\\ & =\underset{\text{与}z\text{无关，期望符号可以去掉}}{\underbrace{{\mathbb{E}}_{z\sim q_{\varphi }}[\ln p_{\theta }(x)]}}+{\mathbb{E}}_{z\sim q_{\varphi }}[\ln p_{\theta }(z|x)]-{\mathbb{E}}_{z\sim q_{\varphi }}[\ln q_{\varphi }(z)]\\ & =\underset{\text{观测数据对数似然/证据}}{\underbrace{\ln p_{\theta }(x)}}+\underset{\text{KL散度}}{\underbrace{{\mathbb{E}}_{z\sim q_{\varphi }}[\ln p_{\theta }(z|x)]-{\mathbb{E}}_{z\sim q_{\varphi }}[\ln q_{\varphi }(z)]}}\\ & =\ell (\theta ;x)-KL(q_{\varphi }(z)||p_{\theta }(z|x))\end{array}\end{array}$$$$\begin{array}{}\text{(5)}& \underset{\text{观测数据对数似然/证据}}{\underbrace{\ell (\theta ;x)}}=\underset{\text{证据下界函数 ELBO}}{\underbrace{\mathcal{L}(q,\theta )}}+\underset{\text{KL散度}}{\underbrace{KL(q_{\varphi }(z)||p_{\theta }(z|x))}}\end{array}$$

观察$(\text{5})$可以发现，当 KL 散度越小，也就是 $q_{\varphi }(z)$ 与后验 $p_{\theta }(z|x)$ 的区别越小时，ELBO 越接近目标对数似然函数。当 KL 散度为 0 时，二者相等，此时就可以完全使用 ELBO 来近似目标函数。而 $\varphi$ 是一个任意的未知分布，所以可以直接令该等式成立。

第二种形式

$$\begin{array}{}\text{(6)}& \begin{array}{rl}\mathcal{L}(q,\theta )& ={\mathbb{E}}_{z\sim q_{\varphi }}[\ln p_{\theta }(x,z)]-{\mathbb{E}}_{z\sim q_{\varphi }}[\ln q_{\varphi }(z))]\\ & ={\mathbb{E}}_{z\sim q_{\varphi }}[\ln p(z)+\ln p_{\theta }(x|z)]-{\mathbb{E}}_{z\sim q_{\varphi }}[\ln q_{\varphi }(z))]\\ & ={\mathbb{E}}_{z\sim q_{\varphi }}[\ln p(z)]+{\mathbb{E}}_{z\sim q_{\varphi }}[\ln p_{\theta }(x|z)]-{\mathbb{E}}_{z\sim q_{\varphi }}[\ln q_{\varphi }(z))]\\ & ={\mathbb{E}}_{z\sim q_{\varphi }}[\ln p_{\theta }(x|z)]+\underset{\text{KL散度}}{\underbrace{{\mathbb{E}}_{z\sim q_{\varphi }}[\ln p(z)]-{\mathbb{E}}_{z\sim q_{\varphi }}[\ln q_{\varphi }(z))]}}\\ & ={\mathbb{E}}_{z\sim q_{\varphi }}[\ln p_{\theta }(x|z)]-\underset{q_{\varphi }(z)\text{和先验}p(z)\text{的KL散度}}{\underbrace{KL(q_{\varphi }(z)||p(z))}}\end{array}\end{array}$$

Note

$x$ 不参与时，$z$ 的分布并不受到参数 $\theta$ 的影响（至少在 VAE 中如此），所以上述推导中，直接将 $p_{\theta }(z)$ 写作了先验 $p(z)$。

从第一种形式的推导中可知，当 $q_{\varphi }(z)=p_{\theta }(z|x)$ 时，$\ell (\theta ;x)=\mathcal{L}(q,\theta )$，即：

$$\begin{array}{}\text{(7)}& \begin{array}{r}\begin{array}{rl}\mathcal{L}(q,\theta )& ={\mathbb{E}}_{z\sim p_{\theta }(z|x)}[\ln p_{\theta }(x|z)]-KL(p_{\theta }(z|x)||p(z))=\ell (\theta ;x)\end{array}\end{array}\end{array}$$

为了便于区分，这里将参数 $\theta$ 进行细分，对于指导 $q(z|x)$ 生成的部分参数，使用 $q_{\varphi }$ 来表示，剩余的参数沿用 $p_{\theta }$ 。最终得到如下 ELBO / 损失函数表达式：

$$\begin{array}{}\text{(8)}& \begin{array}{r}\begin{array}{rl}\mathcal{L}(q,\theta )& =\underset{\text{①重建项（reconstruction term）}}{\underbrace{{\mathbb{E}}_{z\sim q_{\varphi }(z|x)}[\ln p_{\theta }(x|z)]}}-\underset{\text{②先验匹配项（prior matching term）}}{\underbrace{KL(q_{\varphi }(z|x)||p(z))}}\\ & =\ell (\theta ;x)\end{array}\end{array}\end{array}$$

解释

1. 重建项表示了模型重建原始数据 $x$ 的能力。其中，$\ln p_{\theta }(x|z)$ 表示了给定 $z$ ，模型重建出 $x$ 的概率；又因为隐变量是一个随机变量，所以要对 $z$ 求期望，其服从分布的概率密度是后验概率 $q_{\varphi }(z|x)$。
2. 为了极大化目标函数，需要最小化先验匹配项，即使得 $q_{\varphi }(z|x)$ 与 $p(z)$ 尽可能接近，它的作用其实就相当于一个约束或者正则项。

Encode-Decode

Figure 1: Architecture comparison between AE and VAE.

在 VAE 中，假设 $Z$ 服从高斯分布，其先验分布为 $p(z)\sim \mathcal{N}(0,I)$；输出 $X$ 同样也服从高斯分布，并且假设其协方差始终为 $I$。

后验分布-编码器

因为 $Z$ 服从高斯分布，因此其后验分布 $q_{\varphi }(z|x)$ 也是高斯分布，用 ${\mu }_z$ 和 ${\mathrm{\Sigma }}_z$ 来表示其均值和协方差矩阵。编码器做的实际上就是通过输入变量 $x$ 计算得到隐变量 $z$ 的后验分布 $q_{\varphi }(z|x)$ 的均值和方差，而隐变量的值，则由该高斯分布采样得到。后验分布 $q_{\varphi }(z|x)$ 的计算过程取决于参数 $\varphi$ ，这也就是编码器的参数。

生成分布-解码器

与编码器类似，解码器也是从隐变量 $z$ 计算得到输出变量 $x$ 的分布参数。但是为了模型的简单，这里假设输出变量 $x$ 的方差为 $I$，只计算其均值 ${\mu }_x$。计算过程取决于参数 $\theta$，这也就是解码器的参数。

先验匹配项

先验匹配项中的两个概率密度函数可以给出表达式：

$$\begin{array}{}\text{(9)}& \begin{array}{r}\begin{array}{rl}{q}_{\varphi }(z|x)& =\mathcal{N}({\mu }_z,{\mathrm{\Sigma }}_z)\\ p(z)& =\mathcal{N}(0,I)\end{array}\end{array}\end{array}$$

两项都是高斯分布，而两个高斯分布的 KL 散度可以直接得到：

$$\begin{array}{}\text{(10)}& \begin{array}{r}\begin{array}{rl}KL(q_{\varphi }(z|x)||p(z))& =KL(\mathcal{N}({\mu }_z,{\mathrm{\Sigma }}_z)||\mathcal{N}(0,\mathit{\text{I}}))\\ & =\frac{1}{2}(tr({\mathrm{\Sigma }}_z)+{\mu }_z^T{\mu }_z-k-\log det({\mathrm{\Sigma }}_z))\end{array}\end{array}\end{array}$$

损失函数

损失函数的表达式已经给出，但是要作为神经网络训练的损失函数，必须满足：可数值求解，可求导。先验匹配项已经满足，但是计算重建项却存在如下问题：

后验分布 $q_{\varphi }(z|x)$ 的表达式中含有神经网络，无法解析计算期望。可以采用 MCMC 近似求解：

$$\begin{array}{}\text{(11)}& {\mathbb{E}}_{z\sim q_{\varphi }(z|x)}[\ln p_{\theta }(x|z)]\approx \frac{1}{L}\sum _{l=1}^L[\ln p_{\theta }(x|z^{(l)})]\end{array}$$

随机过程不可求导，梯度无法传递。作者使用了重参数化来解决：对于在 $\mathcal{N}\mathcal{(}{\mu }_{\mathcal{z}}\mathcal{,}{\mathcal{\Sigma }}_{\mathcal{z}}\mathcal{)}$ 中采样的值，可以通过 ${\mu }_z+\sqrt{{\mathrm{\Sigma }}_z}\odot ϵ,ϵ\in \mathcal{N}(0,I)$ 来得到。转化后的式子将随机化控制在了一个参数无关的 $ϵ$ 中，从而使得随机采样值可以传递梯度。

解决了以上两个问题后，就可以给出损失函数的最终表达式：

$$\begin{array}{}\text{(12)}& \begin{array}{r}\begin{array}{rl}\mathcal{L}(q,\theta )& =\ell (\theta ;x)=\underset{\text{①对应解码过程}}{\underbrace{{\mathbb{E}}_{z\sim q_{\varphi }(z|x)}[\ln p_{\theta }(x|z)]}}-\underset{\text{②对应编码过程}}{\underbrace{KL(q_{\varphi }(z|x)||p(z))}}\\ & =\frac{1}{L}\sum _{l=1}^L[\ln p_{\theta }(x|z^{(l)})]-KL(\mathcal{N}({\mu }_z,{\mathrm{\Sigma }}_z)||\mathcal{N}(0,\mathit{\text{I}}))\\ & \propto \frac{1}{L}\sum _{l=1}^L[-\frac{1}{2}(x-{\mu }_x{)}^T(x-{\mu }_x)]-\left[\frac{1}{2}(tr({\mathrm{\Sigma }}_z)+{\mu }_z^T{\mu }_z-k-\log det({\mathrm{\Sigma }}_z))\right]\\ & =-\frac{1}{2}\frac{1}{L}\sum _{l=1}^L[(x-{\mu }_x{)}^T(x-{\mu }_x)]-\frac{1}{2}[tr({\mathrm{\Sigma }}_z)+{\mu }_z^T{\mu }_z-k-\log det({\mathrm{\Sigma }}_z)]\\ & \propto -\frac{1}{L}\sum _{l=1}^L\left[\underset{\text{均方误差}}{\underbrace{(x-{\mu }_x{)}^T(x-{\mu }_x)}}\right]-[tr({\mathrm{\Sigma }}_z)+{\mu }_z^T{\mu }_z-k-\log det({\mathrm{\Sigma }}_z)]\\ & \text{其中，}\\ & {\mu }_x={\mu }_{\theta }(z^{(l)})=decoder(z^{(l)})\\ & z^{(l)}={\mu }_z+\sqrt{{\mathrm{\Sigma }}_z}\odot ϵ,ϵ\sim \mathcal{N}(0,\mathit{\text{I}})\\ & {\mu }_z={\mu }_{\varphi }(x)=encoder(x{)}_{{\mu }_z}\\ & {\mathrm{\Sigma }}_z={\mathrm{\Sigma }}_{\varphi }(x)=encoder(x{)}_{{\mathrm{\Sigma }}_z}\end{array}\end{array}\end{array}$$

MHVAE

expand to see details of preliminaries

条件概率密度

条件概率密度函数 $p(y|x)$，准确来说应当是 $p_{Y|X}(y|x)$，指的是在 $X=x$ 的条件下 $Y$ 的概率密度函数。可以通过如下公式计算得到：

$$p_{Y|X}(y|x)=\frac{p_{X,Y}(x,y)}{p_X(x)},p_X(x)>0$$

另一种常见的写法 $P(Y|X)$，则是指在事件 $X$ 发生的条件下，事件 $Y$ 的发生概率。

对于理解 $p_{X,Y}(x,y)=p_{Y|X}(y|x)\cdot p_X(x)$ 的一点：对于 $p(x,y)$ 来说，$x,y$ 都是变量；只是在条件变量中，将 $x$ 视作一个参数进行固定。哪怕x不确定，为输入，我们仍然能够写 py｜x

联合概率密度

联合概率密度 $p_{X,Y}(x,y)$ 被解释为 $X=x$ 且 $Y=y$ 时的概率密度。

对于多元联合分布，有：

$${\displaystyle p_{X_1,\dots ,X_n}(x_1,\dots ,x_n)=p_{X_n|X_1,\dots ,X_{n-1}}(x_n|x_1,\dots ,x_{n-1})p_{X_1,\dots ,X_{n-1}}(x_1,\dots ,x_{n-1})}$$

Figure 2: Architecture of MHVAE.

将 VAE 的过程重复 $T$ 次，无论正向编码还是反向解码，当前时刻步仅与上一时间步相关，就得到了 MHVAE（Markovian Hierarchical Variational Autoencoder）。$q(z_t|z_{t-1})$ 表示了单次编码过程，而 $p(z_{t-1}|z_t)$ 表示了单次解码过程。由于该过程为马尔可夫过程，因此有：

$$\begin{array}{}\text{(13)}& {\displaystyle p_{X_1,\dots ,X_n}(x_1,\dots ,x_n)=p_{X_n|X_{n-1}}(x_n|x_{n-1})p_{X_{n-1}}(x_{n-1})}\end{array}$$

由此，可以得出模型的联合概率分布、隐变量 $z_{1:T}$ 的后验概率分布分别如下：

$$\begin{array}{}\text{(14)}& p(x,z_{1:T})=p(z_T)p_{\theta }(x|z_1)\prod _{t=2}^T{p}_{\theta }(z_{t-1}|z_t)\end{array}$$$$\begin{array}{}\text{(15)}& q_{\varphi }(z_{1:T}|x)=q_{\varphi }(z_1|x)\prod _{t=2}^T{q}_{\varphi }(z_t|z_{t-1})\end{array}$$

与 VAE 的 ELBO 推导过程类似，我们可以得出 MHVAE 的 ELBO：

$$\begin{array}{}\text{(16)}& \begin{array}{r}\begin{array}{rl}\ln p(x)& =\ln \int p(x,z_{1:T})d{z}_{1:T}\\ & =\ln \int \frac{p(x,z_{1:T})q_{\varphi }(z_{1:T}|x)}{q_{\varphi }(z_{1:T}|x)}d{z}_{1:T}\\ & =\ln {\mathbb{E}}_{q_{\varphi }(z_{1:T}|x)}\left[\frac{p(x,z_{1:T})}{q_{\varphi }(z_{1:T}|x)}\right]\\ & \ge {\mathbb{E}}_{q_{\varphi }(z_{1:T}|x)}[\ln \frac{p(x,z_{1:T})}{q_{\varphi }(z_{1:T}|x)}]\end{array}\end{array}\end{array}$$