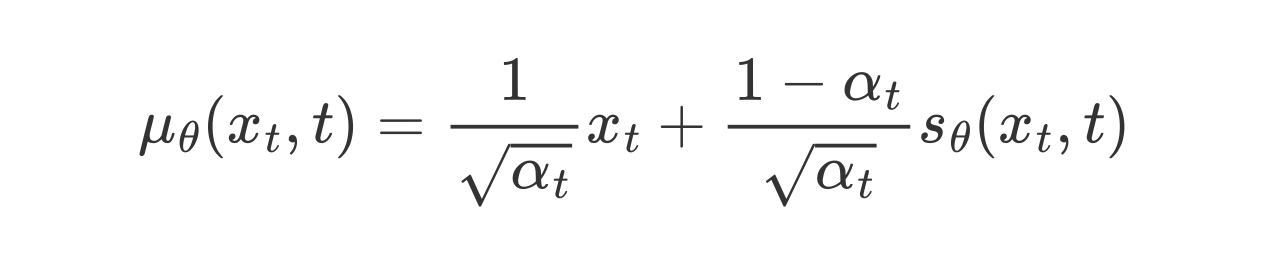DMs[3] Scored-based DDPM

• Paper
• Github Repo

$$$$

Overview

正如 DMs[2] 结尾所提到的，我们可以对 VDM 进行不同的推导，从而得出不同的解释。这里介绍第三种解释方式：score-based DDPM。

Preliminary

这里首先要介绍 Tweedie's Formula：指数族分布的真实均值，可以通过采样样本的经验均值，加上一项修正项进行估计。以 $z\sim \mathcal{N}({\mu }_z,{\mathrm{\Sigma }}_z)$ 为例：

$$\begin{array}{}\text{(1)}& \mathbb{E}[{\mu }_z|z]=z+{\mathrm{\Sigma }}_z{\mathrm{\nabla }}_z\log p_{\text{sample}}(z)\end{array}$$

证明也很简单，假设 $z$ 的采样数量足够，$p_{\text{sample}}\approx p$ ，那么对于观测值 $z$：

$$\begin{array}{}\text{(2)}& \begin{array}{rl}{\mathrm{\nabla }}_z\log p_{\text{sample}}(z)& ={\mathrm{\nabla }}_z\log [\frac{1}{\sqrt{(2\pi {)}^D|{\mathrm{\Sigma }}_z|}}\exp (-\frac{1}{2}(z-{\mu }_z{)}^T{\mathrm{\Sigma }}_z^{-1}(z-{\mu }_z))]\\ & ={\mathrm{\nabla }}_z-\frac{1}{2}(z-{\mu }_z{)}^T{\mathrm{\Sigma }}_z^{-1}(z-{\mu }_z)+\text{const.}\\ & =-{\mathrm{\Sigma }}_z^{-1}(z-{\mu }_z)\end{array}\end{array}$$

代入 (1) 式，容易发现，刚好为 ${\mu }_z$。

Method

Derivation

从 DMs[1] 中可知：

$$\begin{array}{}\text{(3)}& q(x_t|x_0)=\mathcal{N}(x_t;\sqrt{{\overline{\alpha }}_t}{x}_0,(1-{\overline{\alpha }}_t)I)\end{array}$$

结合 Tweedie's Formula，可知：

$$\begin{array}{}\text{(4)}& \mathbb{E}[{\mu }_{x_t}|x_t]=x_t+(1-{\overline{\alpha }}_t){\mathrm{\nabla }}_{x_t}\log p(x_t)\end{array}$$

而我们是知道 $p(x_t)$ 的真实分布的，它由 (3) 式定义。因此，$\mathbb{E}[{\mu }_{x_t}|x_t]$ 恰好是 ${\mu }_{x_t}$，我们可以得到如下等式：

$$\begin{array}{}\text{(5)}& \sqrt{{\overline{\alpha }}_t}{x}_0=x_t+(1-{\overline{\alpha }}_t){\mathrm{\nabla }}_{x_t}\log p(x_t)\end{array}$$$$\begin{array}{}\text{(6)}& x_0=\frac{x_t+(1-{\overline{\alpha }}_t){\mathrm{\nabla }}_{x_t}\log p(x_t)}{\sqrt{{\overline{\alpha }}_t}}\end{array}$$

和 DMs[2] 中一样，我们又可以据此对 ELBO 中的项进行改写。

Denoising matching term

$$\begin{array}{}\text{(7)}& \begin{array}{r}\begin{array}{rl}{\mu }_q(x_t,x_0)& =\frac{\sqrt{{\alpha }_t}(1-{\overline{\alpha }}_{t-1})x_t+\sqrt{{\overline{\alpha }}_{t-1}}(1-{\alpha }_t)x_0}{1-{\overline{\alpha }}_t}\\ & =\frac{1}{\sqrt{{\alpha }_t}}{x}_t+\frac{1-{\alpha }_t}{\sqrt{{\alpha }_t}}\mathrm{\nabla }\log p(x_t)\end{array}\end{array}\end{array}$$

采取与 DPM 中同样的处理思路，对于确定的参数，我们直接令 ${\mu }_{\theta }$ 与之一致。因此，我们可以将 ${\mu }_{\theta }$ 建模如下：

$$\begin{array}{}\text{(6)}& {\mu }_{\theta }(x_t,t)=\frac{1}{\sqrt{{\alpha }_t}}{x}_t+\frac{1-{\alpha }_t}{\sqrt{{\alpha }_t}}{s}_{\theta }(x_t,t)\end{array}$$

因此，denoising matching term 转化为：

$$\begin{array}{}\text{(7)}& \begin{array}{rl}& {\arg min}_{\theta }{D}_{\text{KL}}(q(x_{t-1}|x_t,x_0)||p_{\theta })(x_{t-1}|x_t))\\ =& {\arg min}_{\theta }\frac{1}{2{\sigma }_q^2(t)}\frac{(1-{\alpha }_t{)}^2}{{\alpha }_t}\left[{\Vert s_{\theta }(x_t,t)-{\mathrm{\nabla }}_{x_t}\log p(x_t)\Vert }_2^2\right]\end{array}\end{array}$$

从 (7) 中可知，参数化模型需要学习在 $x_t$ 时的分数 ${\mathrm{\nabla }}_{x_t}\log p(x_t)$。

Reconstruction term

todo

Explanation of score

我们通过 Tweedie's Formula 引入了分数 ${\mathrm{\nabla }}_{x_t}\log p(x_t)$，那么该项在 DPM 中的实际含义是什么呢？回顾 DMs[2] DDPM 中对于 $x_0$ 的重写：

$$\begin{array}{}\text{(8)}& \begin{array}{rl}{x}_0=\frac{x_t+(1-{\overline{\alpha }}_t)\mathrm{\nabla }\log p(x_t)}{\sqrt{{\overline{\alpha }}_t}}& =\frac{x_t-\sqrt{1-{\overline{\alpha }}_t}ϵ}{\sqrt{{\overline{\alpha }}_t}}\\ \therefore (1-{\overline{\alpha }}_t)\mathrm{\nabla }\log p(x_t)& =-\sqrt{1-{\overline{\alpha }}_t}ϵ\\ \mathrm{\nabla }\log p(x_t)& =-\frac{1}{\sqrt{1-{\overline{\alpha }}_t}}ϵ\end{array}\end{array}$$

可以发现，对于真实分布，分数刚好指向了噪声 $ϵ$ 的反向，向着分数的方向步进等价于消除噪声。当然，score function 的提出并不是基于 DPM 模型，相关内容可以查看 SMLD。