SMLD

$$$$

原论文：link

参考博客：link1、link2(封面来源)、link3

Score matching with Langevin dynamics

Basic Idea

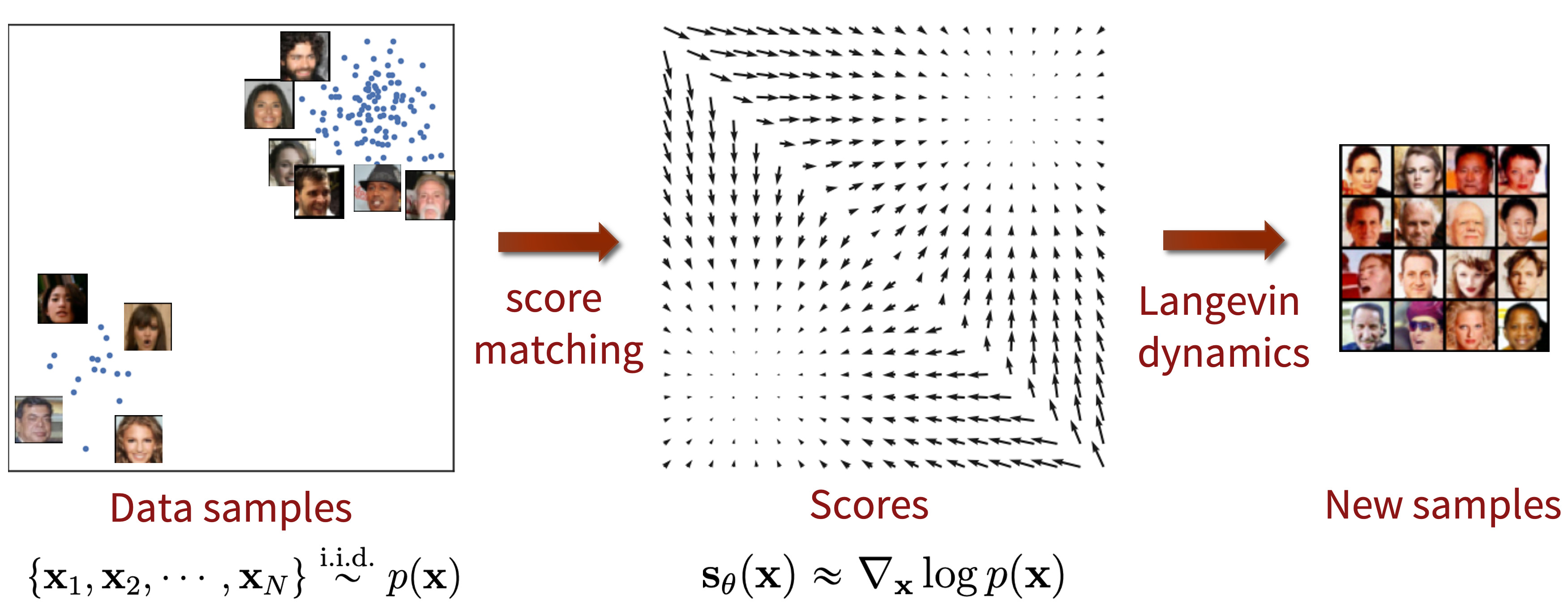
在 DDPM 中，我们通过学习逆向过程的分布 $p_{\theta }({\mathbf{x}}_{t-1}|{\mathbf{x}}_t)$ 来从 $p_T({\mathbf{x}}_T)$ 中生成图像，而基于分数的生成模型给出了另一种思路：放弃使用 $p_{\text{data}}(\mathbf{x})$，转而学习样本分布 $p_{\text{data}}(\mathbf{x})$ 的梯度 ${\mathrm{\nabla }}_{\mathbf{x}}\log p(\mathbf{x})$，随后通过 Langevin dynamics 过程，在 $p_{\text{data}}(\mathbf{x})$中进行采样，以生成新的数据。因此，基于分数的生成模型可以看作由以下两部分构成：

• 通过分数匹配，训练 ${\mathbf{s}}_{\theta }(\mathbf{x})\approx {\mathrm{\nabla }}_{\mathbf{x}}\log p(\mathbf{x})$；
• 通过基于分数的采样算法，随机采样近似 $p_{\text{data}}(\mathbf{x})$ 的样本。

SMLD framework

Score matching

分数匹配方法起初是为了学习具有如下形式的分布：

$$\begin{array}{}\text{(1)}& p_{\theta }(\mathbf{x})=\frac{1}{Z_{\theta }}{e}^{-f_{\theta }(\mathbf{x})}\end{array}$$

其中 $Z_{\theta }=\int e^{-f_{\theta }(\mathbf{x})}$ 是归一项。如果要使用最大似然法，那么就不得不计算 $Z_{\theta }$，而这需要遍历 $\mathbf{x}$，在多数情况下不适用。而该分布的分数 ${\mathrm{\nabla }}_{\mathbf{x}}\log p_{\theta }(\mathbf{x})$ 却很容易计算：

$$\begin{array}{}\text{(2)}& \begin{array}{rl}{\mathrm{\nabla }}_{\mathbf{x}}\log p_{\theta }(\mathbf{x})& ={\mathrm{\nabla }}_{\mathbf{x}}\log \frac{1}{Z_{\theta }}+{\mathrm{\nabla }}_{\mathbf{x}}\log e^{-f_{\theta }(\mathbf{x})}\\ & =-{\mathrm{\nabla }}_{\mathbf{x}}{f}_{\theta }(\mathbf{x})\\ & \approx {\mathbf{s}}_{\theta }(\mathbf{x})\end{array}\end{array}$$

因此，我们可以转而学习该分布的分数，而不需要首先训练一个模型，来预测 $p_{\text{data}}(\mathbf{x})$。而这个方法显然不局限于这种形式的分布。训练该模型，需要最小化均方误差 $\frac{1}{2}\mathbb{E}\left[{\Vert {\mathbf{s}}_{\theta }(\mathbf{x})-{\mathrm{\nabla }}_{\mathbf{x}}\log p_{\text{data}}(\mathbf{x})\Vert }_2^2\right]$，而该损失函数还可以进一步写作与 $p_{\text{data}}$ 无关的形式：

$$\begin{array}{}\text{(3)}& {\mathbb{E}}_{p_{\text{data}}(\mathbf{x})}[\text{tr}({\mathrm{\nabla }}_{\mathbf{x}}{\mathbf{s}}_{\theta }(\mathbf{x})+\frac{1}{2}{\Vert {\mathbf{s}}_{\theta }(\mathbf{x})\Vert }_2^2)]\end{array}$$

expand to see details

（直接挪用了 GPT 的回答）

从以下目标函数形式：

$$J(\theta )=\frac{1}{2}\int p_{\text{data}}(\mathbf{x}){\Vert {\mathbf{s}}_{\text{data}}(\mathbf{x})-{\mathbf{s}}_{\theta }(\mathbf{x})\Vert }_2^2\mathrm{d}\mathbf{x}$$

推导到目标函数的另一种形式：

$$J(\theta )=\int p_{\text{data}}(\mathbf{x})[\mathrm{tr}({\mathrm{\nabla }}_{\mathbf{x}}{\mathbf{s}}_{\theta }(\mathbf{x}))+\frac{1}{2}{\Vert {\mathbf{s}}_{\theta }(\mathbf{x})\Vert }_2^2]\mathrm{d}\mathbf{x}$$

关键步骤如下：

---

原始形式展开

平方项展开：

$${\Vert {\mathbf{s}}_{\text{data}}(\mathbf{x})-{\mathbf{s}}_{\theta }(\mathbf{x})\Vert }_2^2={\Vert {\mathbf{s}}_{\text{data}}(\mathbf{x})\Vert }_2^2-2{\mathbf{s}}_{\text{data}}(\mathbf{x})\cdot s_{\theta }(\mathbf{x})+{\Vert s_{\theta }(\mathbf{x})\Vert }_2^2$$

代入 $J_{\theta }$：

$$J(\theta )=\frac{1}{2}\int p_{\text{data}}(\mathbf{x})({\Vert {\mathbf{s}}_{\text{data}}(\mathbf{x})\Vert }_2^2-2{\mathbf{s}}_{\text{data}}(\mathbf{x})\cdot s_{\theta }(\mathbf{x})+{\Vert {\mathbf{s}}_{\theta }(\mathbf{x})\Vert }_2^2)\mathrm{d}\mathbf{x}$$

拆分为三项：

$$J(\theta )=\frac{1}{2}\int p_{\text{data}}(\mathbf{x}){\Vert {\mathbf{s}}_{\text{data}}(\mathbf{x})\Vert }_2^2\mathrm{d}\mathbf{x}-\int p_{\text{data}}(\mathbf{x}){\mathbf{s}}_{\text{data}}(\mathbf{x})\cdot {\mathbf{s}}_{\theta }(\mathbf{x})\mathrm{d}\mathbf{x}+\frac{1}{2}\int p_{\text{data}}(\mathbf{x}){\Vert {\mathbf{s}}_{\theta }(\mathbf{x})\Vert }_2^2\mathrm{d}\mathbf{x}$$

注意，得分函数 ${\mathbf{s}}_{\text{data}}(\mathbf{x})$ 定义为：

$${\mathbf{s}}_{\text{data}}(\mathbf{x})={\mathrm{\nabla }}_{\mathbf{x}}\log p_{\text{data}}(\mathbf{x})=\frac{p_{\text{data}}(\mathbf{x})}{{\mathrm{\nabla }}_{\mathbf{x}}{p}_{\text{data}}(\mathbf{x})}$$

由此，积分中的第二项可以化简为：

$$\int p_{\text{data}}(\mathbf{x}){\mathbf{s}}_{\text{data}}(\mathbf{x})\cdot {\mathbf{s}}_{\theta }(\mathbf{x})\mathrm{d}\mathbf{x}=\int {\mathrm{\nabla }}_{\mathbf{x}}{p}_{\text{data}}(\mathbf{x})\cdot {\mathbf{s}}_{\theta }(\mathbf{x})\mathrm{d}\mathbf{x}$$

---

利用分部积分化简

对第二项应用分部积分（忽略边界项），有：

$$\int {\mathrm{\nabla }}_{\mathbf{x}}{p}_{\text{data}}(\mathbf{x})\cdot {\mathbf{s}}_{\theta }(\mathbf{x})\mathrm{d}\mathbf{x}=-\int p_{\text{data}}(\mathbf{x})\mathrm{tr}({\mathrm{\nabla }}_{\mathbf{x}}{\mathbf{s}}_{\theta }(\mathbf{x}))\mathrm{d}\mathbf{x}$$

因此：

$$\int p_{\text{data}}(\mathbf{x}){\mathbf{s}}_{\text{data}}(\mathbf{x})\cdot {\mathbf{s}}_{\theta }(\mathbf{x})\mathrm{d}\mathbf{x}=-\int p_{\text{data}}(\mathbf{x})\mathrm{tr}({\mathrm{\nabla }}_{\mathbf{x}}{\mathbf{s}}_{\theta }(\mathbf{x}))\mathrm{d}\mathbf{x}$$

• 为什么能省略边界项 $p_{\text{data}}(\mathbf{x})\cdot {\mathbf{s}}_{\theta }(\mathbf{x})$ ? 在分部积分中，边界项其实是 $p_{\text{data}}(\mathbf{x})\cdot {\mathbf{s}}_{\theta }(\mathbf{x}){|}_a^b$，而在真实分布中，$a,b$ 两点的概率密度基本为0。
• 为什么是 $\text{tr}$ ? 由向量场 $v(x)$ 的散度定义。

---

代入原表达式

将化简结果代入 $J(\theta )$：

$$J(\theta )=\frac{1}{2}\int p_{\text{data}}(\mathbf{x}){\Vert {\mathbf{s}}_{\text{data}}(\mathbf{x})\Vert }_2^2\mathrm{d}\mathbf{x}+\int p_{\text{data}}(\mathbf{x})\mathrm{tr}({\mathrm{\nabla }}_{\mathbf{x}}{\mathbf{s}}_{\theta }(\mathbf{x}))\mathrm{d}\mathbf{x}+\frac{1}{2}\int p_{\text{data}}(\mathbf{x}){\Vert {\mathbf{s}}_{\theta }(\mathbf{x})\Vert }_2^2\mathrm{d}\mathbf{x}$$

注意到，第一项是与参数 $\theta$ 无关的常数，可以忽略。

因此：

$$J(\theta )=\int p_{\text{data}}(\mathbf{x})\mathrm{tr}({\mathrm{\nabla }}_{\mathbf{x}}{\mathbf{s}}_{\theta }(\mathbf{x}))\mathrm{d}\mathbf{x}+\frac{1}{2}\int p_{\text{data}}(\mathbf{x}){\Vert {\mathbf{s}}_{\theta }(\mathbf{x})\Vert }_2^2\mathrm{d}\mathbf{x}$$

整理后为：

$$\begin{array}{rl}J(\theta )& =\int p_{\text{data}}(\mathbf{x})[\mathrm{tr}({\mathrm{\nabla }}_{\mathbf{x}}{\mathbf{s}}_{\theta }(\mathbf{x}))+\frac{1}{2}{\Vert {\mathbf{s}}_{\theta }(\mathbf{x})\Vert }_2^2]\mathrm{d}\mathbf{x}\\ & ={\mathbb{E}}_{p_{\text{data}}(\mathbf{x})}[\mathrm{tr}({\mathrm{\nabla }}_{\mathbf{x}}{\mathbf{s}}_{\theta }(\mathbf{x}))+\frac{1}{2}{\Vert {\mathbf{s}}_{\theta }(\mathbf{x})\Vert }_2^2]\end{array}$$

但是，$\text{tr}({\mathrm{\nabla }}_{\mathbf{x}}{\mathbf{s}}_{\theta }(\mathbf{x}))$ 的计算成本很高（因为是二阶偏导），针对这个问题，有两种解决方法：

Denoising score matching

这类方法可以完全绕开 $\text{tr}({\mathrm{\nabla }}_{\mathbf{x}}{\mathbf{s}}_{\theta }(\mathbf{x}))$ 的计算，通过向原始分布 $p_{\text{data}}(\mathbf{x})$ 添加噪声 $q_{\sigma }(\tilde{\mathbf{x}}\mid \mathbf{x})$，我们可以得到新的分布 $q_{\sigma }(\tilde{\mathbf{x}})\triangleq \int q_{\sigma }(\tilde{\mathbf{x}}\mid \mathbf{x})p_{\text{data}}(\mathbf{x})\mathrm{d}\mathbf{x}$，等价的。而可以证明，对于 $q_{\sigma }(\tilde{\mathbf{x}})$ 的目标函数等价于：

$$\begin{array}{}\text{(3)}& \frac{1}{2}{\mathbb{E}}_{q_{\sigma }(\tilde{\mathbf{x}}\mid \mathbf{x})p_{\text{data}}(\mathbf{x})}\left[{\Vert {\mathbf{s}}_{\theta }(\tilde{\mathbf{x}})-{\mathrm{\nabla }}_{\tilde{\mathbf{x}}}\log q_{\sigma }(\tilde{\mathbf{x}}\mid \mathbf{x})\Vert }_2^2\right]\end{array}$$

这个目标函数具有以下特点：

• 同样与 $p_{\text{data}}$ 无关，方便计算；
• 最终得到的是 ${\mathbf{s}}_{{\theta }^{\ast }}={\mathrm{\nabla }}_{\mathbf{x}}\log q_{\sigma }(\tilde{\mathbf{x}}\mid \mathbf{x})\approx \log p_{\text{data}}(\mathbf{x})$，这要求添加的扰动程度不能太大。

Sliced score matching

使用随机投影来近似计算 $\text{tr}({\mathrm{\nabla }}_{\mathbf{x}}{\mathbf{s}}_{\theta }(\mathbf{x}))$，目标函数为

$$\begin{array}{}\text{(4)}& {\mathbb{E}}_{p_{\mathbf{v}}}{\mathbb{E}}_{p_{\text{data}}(x)}\left[{\mathbf{v}}^T{\mathrm{\nabla }}_{\mathbf{x}}{\mathbf{s}}_{\theta }(\mathbf{x})\mathbf{v}+\frac{1}{2}{\Vert {\mathbf{s}}_{\theta }(\mathbf{x})\Vert }_2^2\right]\end{array}$$

Langevin dynamics

朗之万动力采样（Langevin dynamics sample，后简记为 $\mathcal{LD}$）算法可以从 $p(\mathbf{x})$ 中生成样本，而只需要用到分布的分数。首先，从某个已知的先验分布 $\pi (\mathbf{x})$ 中采样 ${\tilde{\mathbf{x}}}_0\sim \pi (\mathbf{x})$，然后迭代如下过程：

$$\begin{array}{}\text{(5)}& {\tilde{\mathbf{x}}}_t={\tilde{\mathbf{x}}}_{t-1}+\frac{ϵ}{2}{\mathrm{\nabla }}_{\mathbf{x}}\log {\tilde{\mathbf{x}}}_{t-1}(+)\sqrt{ϵ}{\mathbf{z}}_t\end{array}$$

因此，我们可以首先通过分数匹配训练 ${\mathbf{s}}_{\theta }(\mathbf{x})\approx {\mathrm{\nabla }}_{\mathbf{x}}\log p({\tilde{\mathbf{x}}}_{t-1})$ ， 随后通过 $\mathcal{LD}(T\to \mathrm{\infty },ϵ\to 0)$ 来生成样本。

Challenges of naive SMLD

流形假设

在实际情况中，样本可能集中在高维样本空间的低维流形上 (某些维度不包含信息，例如全是0)，这会导致 SMLD 做法的一些问题。首先，${\mathrm{\nabla }}_{\mathbf{x}}$ 在无效维度上无法定义；其次，当数据无法填满空间时，还会导致 ${\mathbf{s}}_{\theta }(\mathbf{x})$ 预测不一致。

低密度区域

在概率密度较低的区域，我们能获取的样本相应的也会更少，这会导致训练不足；

无法处理混合分布

对于一个分布 $p_{\text{data}}(\mathbf{x})$，我们称 $\{\mathbf{x}\mid p_{\text{data}}(\mathbf{x})>0\}$ 为其支持集，其中每个点称为一个 mode。假设有一个混合分布 $p(\mathbf{x})=\pi p_1(\mathbf{x})+(1-\pi )p_2(\mathbf{x})$，在 $p_1(\mathbf{x})$ 的支持集中，我们有 ${\mathrm{\nabla }}_{\mathbf{x}}\log x(=){\mathrm{\nabla }}_{\mathbf{x}}\log \pi +\log p_1(\mathbf{x})={\mathrm{\nabla }}_{\mathbf{x}}\log p_1(\mathbf{x})$ ，可以发现梯度与混合系数 $\pi$ 无关。在 $p_2(\mathbf{x})$ 的支持集中，也能得出类似的结论。这就意味着，生成样本的过程并不会取决于 $\pi$。假设我们在空间内随机采样初始点，因为生成过程与 $\pi$ 无关，这会导致最终生成的样本均匀分布在各 mode 上。同时，当各 mode 之间存在低密度区域时，也会导致 $\mathcal{LD}$ 需要需要很小的步长、很大的迭代次数，才能正确采样。（个人理解：正确的 $\mathcal{LD}$ 应当能够实现跨 mode 生成，否则样本的生成将取决于其初始点的选取，这显然不是 $p_{\text{data}}(\mathbf{x})$，而是一个取决于 ${\mathbf{x}}_0$ 的条件分布。而 SMLD 忽略混合系数 $\pi$ 的特性会导致在跨域低密度区域时困难，进而导致跨 mode 困难。较小的步长是为了稳定，否则会跳过 mode。）

Warning

对于流形导致的两个问题、$\mathcal{LD}$ 在低密度区域存在时的问题，笔者暂时还不能完全理解，所以表述可能并不准确。如果你在读这篇笔记，请务必查看原论文。

NCSN

Inspiration

基于上述问题，原论文作者提出了 NCSN(Noise Conditional Score Networks)。该方法的提出基于以下观察：

• 加入噪声可以解决上述问题：加噪会改变原有的数据分布：$p_{\sigma }(\tilde{\mathbf{x}})=\int p_{\sigma }(\tilde{\mathbf{x}}\mid \mathbf{x})p_{\text{data}}(\mathbf{x})\mathrm{d}\mathbf{x}$，当噪声足够大时，我们甚至可以使得 $p_{\sigma }(\tilde{\mathbf{x}})\approx \pi (\mathbf{x})$，变成一个已知的先验分布。最直接的，加噪可以解决流型假设问题和低密度区域问题；而对于混合分布问题，原文并没有给出详细的解释，个人理解应当也和低密度区域的消除有关。
• 较小的噪声水平可以使得学习到的 ${\mathbf{s}}_{\theta }(\mathbf{x})$ 与 ${\mathrm{\nabla }}_{\mathbf{x}}\log p_{\text{data}}(\mathbf{x})$ 足够接近，不会影响生成结果。

显然，这两个诉求是冲突的。那就设置不同强度的噪声，并且让模型同时学习不同强度下的 ${\mathbf{s}}_{\theta }$。

Definition

令 $\{{\sigma }_i{\}}_{i=1}^L$ 为满足 $\frac{{\sigma }_1}{{\sigma }_2}=\cdots =\frac{{\sigma }_{L-1}}{{\sigma }_L}>1$ 的正几何序列。给定噪声 $\sigma$，加噪后的分布为

$$\begin{array}{}\text{(6)}& q_{\sigma }(\mathbf{x})\triangleq \int p_{\text{data}}(t)\mathcal{N}(\mathbf{x};t,{\sigma }^{2}I)\mathrm{d}t\end{array}$$

其中，设置 ${\sigma }_1$ 足够大，使得加噪后的分布能够克服上述的问题； 设置 ${\sigma }_L$ 足够小，使得噪声对生成结果的影响足够小。而模型的训练目标针对所有噪声的：

$$\begin{array}{}\text{(7)}& \mathrm{\forall }\sigma \in \{{\sigma }_i{\}}_{i=1}^L{\mathbf{s}}_{\theta }(\mathbf{x},\sigma )\approx {\mathrm{\nabla }}_{\mathbf{x}}\log q_{\sigma }(\mathbf{x})\end{array}$$

称 ${\mathbf{s}}_{\theta }(\mathbf{x},\sigma )$ 为一个 NCSN。

Train and Inference

训练过程以 denoising score matching 为例：加噪过程 $q_{\sigma }(\tilde{\mathbf{x}}\mid \mathbf{x})=\mathcal{N}(\tilde{\mathbf{x}};\mathbf{x},{\sigma }^{2}I)$，因此 ${\mathrm{\nabla }}_{\tilde{\mathbf{x}}}\log q_{{\sigma }_i}(\tilde{\mathbf{x}}\mid x)=-(\tilde{\mathbf{x}}-\mathbf{x})/{\sigma }_i^2$，代入 (3) 式可知：

$$\begin{array}{}\text{(8)}& \begin{array}{r}\ell (\theta ;{\sigma }_i)\triangleq \frac{1}{2}{\mathbb{E}}_{p_{\text{data}}(\mathbf{x})}{\mathbb{E}}_{\tilde{\mathbf{x}}\sim \mathcal{N}(\mathbf{x},{\sigma }^2,I)}\left[{\Vert {\mathbf{s}}_{\theta }(\tilde{\mathbf{x}},\sigma )+\frac{\tilde{\mathbf{x}}-\mathbf{x}}{{\sigma }^2}\Vert }_2^2\right]\end{array}\end{array}$$

再对所有的 ${\sigma }_i$ 统一处理，可得：

$$\begin{array}{}\text{(9)}& \mathcal{L}(\theta ;\{{\sigma }_i{\}}_{i=1}^L)\triangleq \frac{1}{L}\sum _{i=1}^L\lambda ({\sigma }_i)\ell (\theta ;{\sigma }_i)\end{array}$$

推理过程可以看作 $\mathcal{LD}$ 的改良版，文章中称为 "annealed Langevin dynamics"，其实就是在不同的噪声水平上进行相应的 $\mathcal{LD}$。

Figure 1: Annealed Langevin dynamics.