GMs with SDE

$$$$

原论文：link

参考博客：link1，link2，link3

前排提醒：这篇文章的内容可谓是丰俭由人，在正文部分，作者仅仅介绍了使用 SDE 建模生成过程的框架，而更一般的情况、推导过程中使用的结论，在附录中都有详细的推导。所以，在本笔记中，会直接使用一系列结论，一方面是因为笔者暂时没时间、没能力学习所有延伸出的知识点，另一方面，列出每个结论的出处过于繁琐。因此，仅列出相关的附录，有兴趣可以自行查阅原论文。

SDE

Forward & Reverse Process

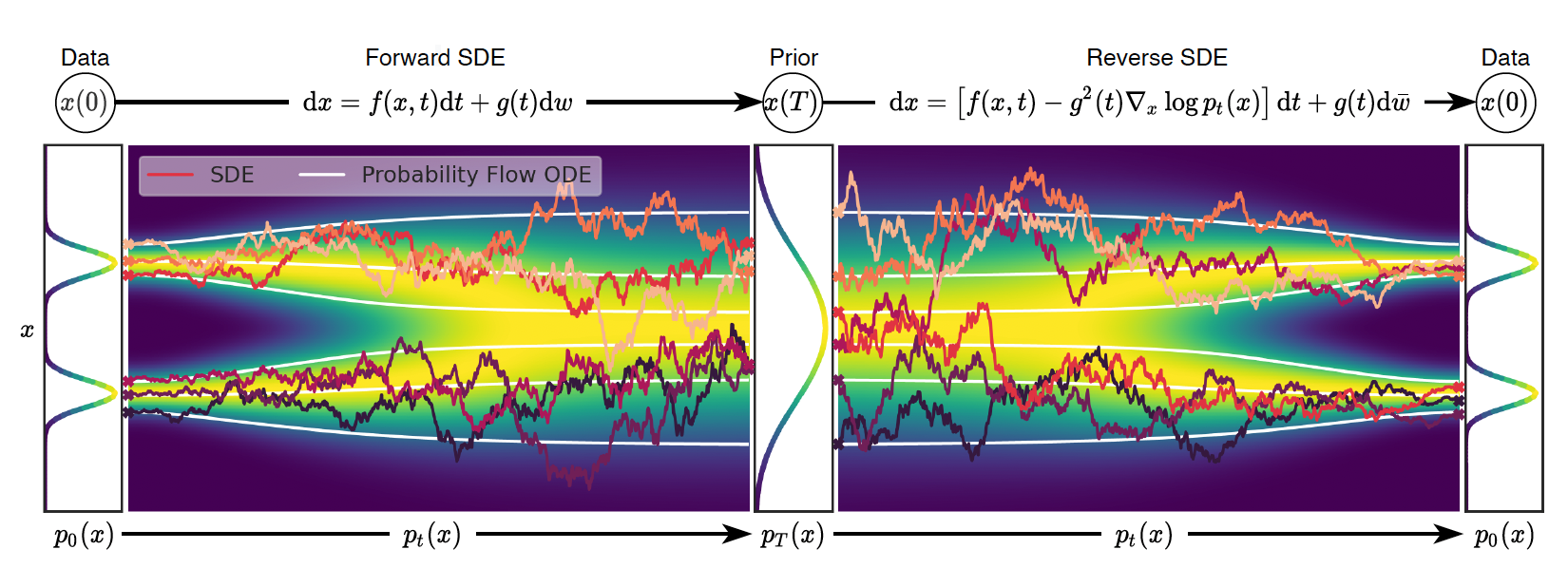
扩散过程可以看作是经过如下的过程，将样本从 $\mathbf{x}(0)\sim p_{\text{data}}$ 转换到先验分布 $\mathbf{x}(T)\sim p_T$：

$$\begin{array}{}\text{(1)}& \mathrm{d}\mathbf{x}=\mathbf{f}(\mathbf{x},t)\mathrm{d}t+g(t)\mathrm{d}\mathbf{w}\end{array}$$

其中：$\mathbf{w}$ 是标准温拿过程，$\mathbf{f}(\cdot ,t)$ 叫做 $\mathbf{x}(t)$ 的漂移系数，$g(\cdot )$ 是扩散系数（这里为了简化模型，假设其与实践无关，在原论文附录 A 中有对于一般情况 $g(\cdot ,t)$ 的推导）。我们可以写出 $\mathbf{x}(t)$ 的概率密度函数，记作 $p_t(\mathbf{x})$，而 $\mathbf{x}(s)$ 到 $\mathbf{x}(t)$ 的转移核记作 $p_{st}(\mathbf{x}(t)\mid \mathbf{x}(s))$。

将前向过程反过来，就可以得到生成过程。而使用 SDE 建模的一大好处是，有现成的结论可以使用，可以直接写出逆向过程的表达式：

$$\begin{array}{}\text{(2)}& \mathrm{d}\mathbf{x}=[\mathbf{f}(\mathbf{x},t)-g(t{)}^2{\mathrm{\nabla }}_{\mathbf{x}}\log p_t(\mathbf{x})]\mathrm{d}t+g(t)\mathrm{d}\overline{\mathbf{w}}\end{array}$$

$\overline{\mathbf{w}}$ 是时间逆向时的标准温拿过程，而 $\mathrm{d}t$ 是一个负的时间步。在 (2) 中，只有 ${\mathrm{\nabla }}_{\mathbf{x}}\log p_t(\mathbf{x})$ 是未知项，而处理这一项的方法也应该很熟悉了，我们可以训练如下模型：

$$\begin{array}{}\text{(3)}& {\theta }^{\ast }={\arg min}_{\theta }{\mathbb{E}}_t\{\lambda (t){\mathbb{E}}_{\mathbf{x}(0)}{\mathbb{E}}_{\mathbf{x}(t)|\mathbf{x}(0)}\left[{\Vert {\mathbf{s}}_{\theta }(\mathbf{x}(t),t)-{\mathrm{\nabla }}_{\mathbf{x}(t)}\log p_{0t}(\mathbf{x}(t)\mid \mathbf{x}(0))\Vert }_2^2\right]\}\end{array}$$

Interpretation of SMLD and DDPM

详细推导可见附录 B。

SMLD

对于噪声水平 ${\sigma }_i$，有 $p_{{\sigma }_i}(\mathbf{x}\mid {\mathbf{x}}_0)=\mathcal{N}(\mathbf{x};{\mathbf{x}}_0,{\sigma }_i^{2}I)$，即 $\mathbf{x}={\mathbf{x}}_0+{\sigma }_i\mathcal{N}(0,I)$ 。因此，对于从 ${\sigma }_i$ 和 ${\sigma }_{i-1}$ 中采样的样本，有如下递推式：

$$\begin{array}{}\text{(4)}& {\mathbf{x}}_i={\mathbf{x}}_{i-1}+\sqrt{{\sigma }_i^2-{\sigma }_{i-1}^2}{\mathbf{z}}_{i-1}i=1,\dots ,N\end{array}$$

当 $N\to \mathrm{\infty },\mathrm{\Delta }t\to 0$ 时，可以将该过程写成 SDE 的形式：

$$\begin{array}{}\text{(5)}& \mathrm{d}\mathbf{x}=\sqrt{\frac{\mathrm{d}[{\sigma }^2(t)]}{\mathrm{d}t}}\mathrm{d}\mathbf{w}\end{array}$$

当 $t\to \mathrm{\infty }$ 时，有 $\mathrm{\Sigma }(t)\to \mathrm{\infty }$，因此叫做 Variance Exploding(VE) SDE。

DDPM

$$\begin{array}{}\text{(6)}& {\mathbf{x}}_i=\sqrt{1-{\beta }_i}{\mathbf{x}}_{i-1}+\sqrt{{\beta }_i}{\mathbf{z}}_{i-1}i=1,\dots ,N\end{array}$$

当 $N\to \mathrm{\infty },\mathrm{\Delta }t\to 0$ 时，可以将该过程写成 SDE 的形式：

$$\begin{array}{}\text{(7)}& \mathrm{d}\mathbf{x}=-\frac{1}{2}\beta (t)\mathrm{d}t+\sqrt{\beta (t)}\mathrm{d}\mathbf{w}\end{array}$$

当 $t\to \mathrm{\infty }$ 时，有 $\mathrm{\Sigma }(t)=I+e^{{\int }_0^t-\beta (s)\mathrm{d}s}(\mathrm{\Sigma }(0)-I)\to \text{const}$，因此叫做 Variance Preserving(VP) SDE。

一个疑点

对于推导中暂时有两步不明白：

原文推导过程.

1. 对于 (24) 式，有 ：

   $$\beta (t+\mathrm{\Delta }t)\mathrm{\Delta }t={\overline{\beta }}_{Nt+N\mathrm{\Delta }t}\mathrm{\Delta }t={\overline{\beta }}_{Nt+1}\mathrm{\Delta }t=N{\beta }_{Nt+1}\cdot \frac{1}{N}={\beta }_{Nt+1}$$

   而 ${\beta }_{Nt+1}$ 并没有无穷小的条件，则第一步近似无法成立。

2. $\sqrt{\mathrm{\Delta }t}\mathbf{z}(t)\approx \mathrm{d}\mathbf{w}$ 是由温拿过程定义的吗？

sub-VP SDEs

基于 VP SDES，作者提出了一类新的 SDE，sub-VP SDE：

$$\begin{array}{}\text{(8)}& \mathrm{d}\mathbf{x}=-\frac{1}{2}\beta (t)\mathbf{x}\mathrm{d}t+\sqrt{\beta (t)(1-e^{2{\int }_0^t-\beta (s)\mathrm{d}s})}\mathrm{d}\mathbf{w}\end{array}$$

sub-VP SDE 的方差上界总是对应的 SDE。

conclusion

上述三种 SDE 的漂移系数均是 affine 的，因此它们的转移核 $p_{0t}(\mathbf{x}(t)\mid \mathbf{x}(0))$ 都是高斯分布，并且可以计算如下：

$$\begin{array}{}\text{(9)}& p_{0t}(\mathbf{x}(t)\mid \mathbf{x}(0))=\{\begin{array}{ll}\mathcal{N}(\mathbf{x}(t);\mathbf{x}(0),[{\sigma }^2(t)-{\sigma }^2(0)]\mathbf{I}),& \text{(VE SDE)}\\ \mathcal{N}(\mathbf{x}(t);\mathbf{x}(0)e^{-\frac{1}{2}{\int }_0^t\beta (s)ds},\mathbf{I}-\mathbf{I}{e}^{-{\int }_0^t\beta (s)ds}),& \text{(VP SDE)}\\ \mathcal{N}(\mathbf{x}(t);\mathbf{x}(0)e^{-\frac{1}{2}{\int }_0^t\beta (s)ds},{[1-e^{-{\int }_0^t\beta (s)ds}]}^2\mathbf{I}),& \text{(sub-VP SDE)}\end{array}\end{array}$$

有了确定的表达式，我们就可以利用 (3) 对模型进行训练

Solving the Reverse SDE

SDE solvers

训练得到 ${\mathbf{s}}_{\theta }$ 后，我们就可以模拟逆向 SDE，来从 $p_0$ 中生成样本。作者在文中介绍了四种方法：

一般性的数值方法

归根结底，这是一个微分方程，因此可以使用数值方法来求解，例如 Euler-Maruyama 、stochastic Runge-Kutta methods，这些方法等价于对 SDE 采用了相应的离散化处理。

ancestral sampling

这种方法来源于 score-based DDPM 推导中的逆向过程：

$$\begin{array}{}\text{(10)}& {\mathbf{x}}_{i-1}=\frac{1}{\sqrt{1-{\beta }_i}}({\mathbf{x}}_i+{\beta }_i{\mathbf{s}}_{{\theta }^{\ast }}({\mathbf{x}}_i,i))+\sqrt{{\beta }_i}{\mathbf{z}}_i\end{array}$$

之所以叫这个名字，是因为它实际上是在 $\prod _{i=1}^N{p}_{\theta }({\mathbf{x}}_{i-1}\mid {\mathbf{x}}_i)$ 中采样。这种方法源自 DDPM，但在应用到其他 SDE 的时候可能存在困难（但实际上作者成功应用到了 VE SDE，详见附录 F）。

reverse diffusion

为了解决 ancestral sampling 的问题，作者提出了 reverse diffusion（详见附录 E），可以在给定前向过程的离散化情况下，给出相应的逆向过程离散化。

probability flow

对于给定的 SDE，作者推导出了相应的 probability flow ODE（详见附录 D），他们具有相同的边缘分布 $\{p_t(\mathbf{x}){\}}_{t=0}^T$ ，其表达式如下：

$$\begin{array}{}\text{(11)}& \mathrm{d}\mathbf{x}=[\tilde{\mathbf{f}}(\mathbf{x},t)-\frac{1}{2}g(t{)}^2{\mathrm{\nabla }}_{\mathbf{x}}\log p_t(\mathbf{x})]\mathrm{d}t\end{array}$$

相比原始的反向 SDE (2)，直观上是将 $\mathrm{d}\overline{\mathbf{w}}$ 给吸收进了 $\tilde{\mathbf{f}}(\mathbf{x},t)$。效果上讲，最直接的，probability flow ODE 可以加快采样速度，文章提到可以减少超过 90% 的计算。

Table 1. 不同 solver，sampler 的生成结果. PC1000 指的是预测和修正分别 1000 步.

Predictor-Corrector Samplers

除了对于 (2) 的采用不同离散化方法，作者还提出了 PC 采样来作用于所有 solver，以改进生成效果。而实际效果也确实很好：如 表1 所示，使用 PC 采样，可以使得 probability flow ODE 的效果接近其他的 solver。

在 PC 采样 中，predictor 可以是任何离散化的反向 SDE，而 corrector 可以是任何基于分数的 MCMC 方法。以 reverse diffusion SDE 和退火朗之万动力采样为例，可以针对 VE SDE 和 VP SDE 分别得出如下算法：

Figure 1. PC sampling for VE/VP SDE.

为什么需要 PC 采样？注意到，对于逆向 SDE 的离散化难免会有误差，在进行一步预测后，通过多步朗之万动力采样，可以一定程度上修正该误差。引入的修正步骤会增加计算开销，而 ODE 加上修正步骤，还能维持多少的计算量削减？

Controllable Generation

可控生成是指，不从 $p_0({\mathbf{x}}_0)$ 中采样，而是从 $p_0(\mathbf{x}(0)\mid \mathbf{y})$ 中采样，其中 $\mathbf{y}$ 可以是文字描述、类别信息等等。为了求解条件化的逆向 SDE，实际上只需要表示出 (2) 中的 ${\mathrm{\nabla }}_{\mathbf{x}}\log p_t(\mathbf{x}\mid \mathbf{y})$。根据贝叶斯定理可知：

$$\begin{array}{}\text{(12)}& {\mathrm{\nabla }}_{\mathbf{x}}\log p_t(\mathbf{x}\mid \mathbf{y})={\mathrm{\nabla }}_{\mathbf{x}}[\log p_t(\mathbf{x})+\log p_t(\mathbf{y}\mid \mathbf{x})-\log p_t(\mathbf{y})]={\mathrm{\nabla }}_{\mathbf{x}}[\log p_t(\mathbf{x})+\log p_t(\mathbf{y}\mid \mathbf{x})]\end{array}$$

代入 (2)，可以得到条件化逆向 SDE 的表达式：

$$\begin{array}{}\text{(13)}& \mathrm{d}\mathbf{x}=\{\mathbf{f}(\mathbf{x},t)-g(t{)}^2[{\mathrm{\nabla }}_{\mathbf{x}}\log p_t(\mathbf{x})+{\mathrm{\nabla }}_{\mathbf{x}}\log p_t(\mathbf{y}\mid \mathbf{x})]\}\mathrm{d}t+g(t)d\overline{\mathbf{w}}\end{array}$$

至于 $p_t(\mathbf{y}\mid \mathbf{x}(t))$，即给定样本 $\mathbf{x}(t)$，能够输出其“类别”的概率，应当是事先训练好的分类器。