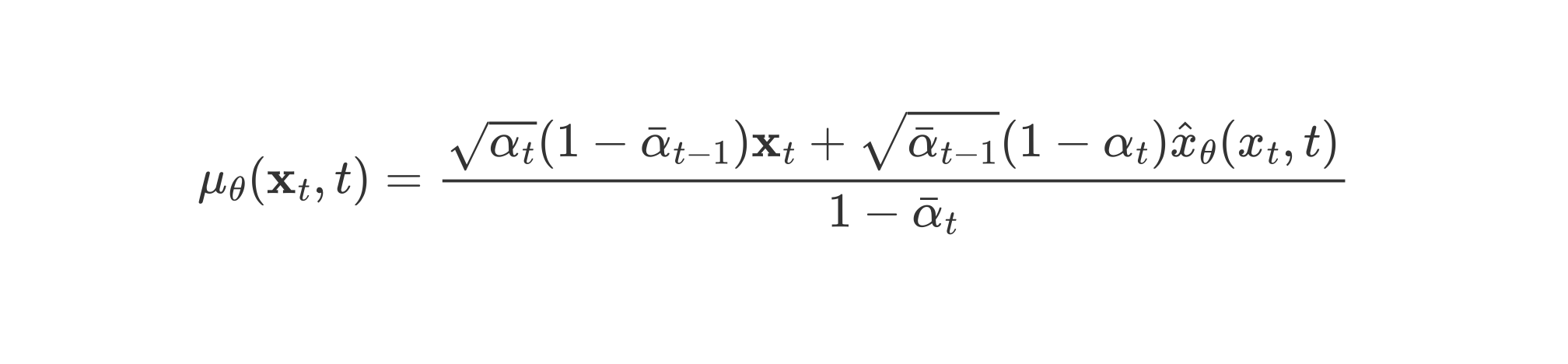DMs[1] DPM

Overview

Figure 1: Architecture of VDM.

VDM 的原理与 MHVAE 非常类似，可以看作是在 MHVAE 的基础上添加了如下 3 个限制条件得到：

• 隐变量 $z_i$ 的维度与输入输出 $x$ 的维度一致。因此，不再使用 $z_i$ ，而统一使用 $x_i(0⩽i⩽T)$ 来表示所有的变量。
• 编码器 $q(x_t|x_{t-1})$ 不再是通过神经网络学习的过程，而是一个固定的高斯线性变换。
• 通过为编码器的一系列高斯线性变换设置系数，使得最终的 $x_T$ 收敛到 $\mathcal{N}(0,I)$。

前向过程

给定一个真实输入 $x_0$，通过逐步添加噪声，最终得到 $x_T\sim \mathcal{N}(0,I)$ ，因此也叫作扩散过程。整个模型的后验分布可以写作：

$$\begin{array}{}\text{(1)}& q(x_{1:T}|x_0)=\prod _{t=1}^{T}q(x_t|x_{t-1})\end{array}$$

而由于编码器不再是一个参数化的过程，所以 $q(x_t|x_{t-1})$ 可以用公式明确给出：

$$\begin{array}{}\text{(2)}& q(x_t|x_{t-1})=\mathcal{N}(\sqrt{{\alpha }_t}{x}_{t-1},(1-{\alpha }_t)\mathit{\text{I}})\end{array}$$

逆向过程

从随机高斯噪声 $x_T$ 开始，逐步还原出有意义的数据。整个模型的联合概率可以写作：

$$\begin{array}{}\text{(3)}& p(x_{0:T})=p(x_T)\prod _{t=T-1}^{0}p(x_t|x_{t+1})\end{array}$$

其中，根据模型假设，我们知道 $p(x_T)\sim \mathcal{N}(0,I)$。那么，我们能否直接给出 $p(x_t|x_{t+1})$ 的表达式呢？

$$\begin{array}{}\text{(4)}& \begin{array}{rl}p(x_t|x_{t+1})& =\frac{q(x_{t+1}|x_t)\cdot p(x_t)}{p(x_{t+1})}\mathrm{贝}\mathrm{叶}\mathrm{斯}\mathrm{定}\mathrm{理}\\ & =\frac{q(x_{t+1}|x_t)\cdot p(x_t)}{\int q(x_{t+1}|x_t)p(x_t)\mathrm{d}{x}_t}\mathrm{利}\mathrm{用}{x}_{t+1}\mathrm{对}{x}_t\mathrm{的}\mathrm{条}\mathrm{件}\mathrm{概}\mathrm{率}\mathrm{求}\mathrm{出}p(x_{t+1})\end{array}\end{array}$$

观察其中的各项：

1. $q(x_{t+1}|x_t)$：该项是前向过程的加噪过程，可以写出表达式；
2. $p(x_t)$：该项表示了 $t$ 时样本的边缘概率密度函数，可以从 $p(x_0)$ 迭代计算得到。但 $p(x_0)$ 对逆向过程来说不可知（即便是通过采样来模拟）；
3. $\int q(x_{t+1}|x_t)p(x_t)\mathrm{d}{x}_t$：该项表示了 $t+1$ 时样本服从的概率密度函数，需要对 $x_t$ 的各种取值进行遍历积分，对于图像来说，这显然不可行。

因此，我们没法直接给出 $p(x_t|x_{t+1})$ 的表达式。而扩散模型借助参数化近似（如神经网络）来学习逆过程分布。

另一种想法是，基于 (2)，对其进行重参数化，可以得到：

$$x_t=\sqrt{{\alpha }_t}{x}_{t-1}+(1-{\alpha }_t)ϵ$$

移项之后，不就可以得出 $p(x_t\mid x_{t+1})$ 了吗？

这里搬一下 路橙大佬的解答，（目前get的）大致意思是：高斯分布对应的重参数化结果 $x_t=f(x_{t-1},ϵ)$ 中，这两个变量应当是相互独立的，而反解结果中，$x_t$ 与 $ϵ$ 不再独立，所以即使写成了重参数化形式，也不能逆推回高斯分布。而这里的 $ϵ(x_t)$ 也是具有实际含义的，它就是 DDPM 想要预测的噪声 ${\widehat{ϵ}}_{\theta }(x_t,t)$

ELBO

Vanilla ELBO

VDM 可以通过最大化 ELBO 来进行优化：

$$\begin{array}{}\text{(5)}& \begin{array}{r}\begin{array}{rl}\ln p(x_0)& =\ln \int p(x_{0:T})\mathrm{d}{x}_{1:T}\mathrm{边}\mathrm{际}\mathrm{化}\\ & =\ln \int \frac{p(x_{0:T})q(x_{1:T}|x_0)}{q(x_{1:T}|x_0)}\mathrm{d}{x}_{1:T}\\ & =\ln {\mathbb{E}}_{q(x_{1:T}|x_0)}\left[\frac{p(x_{0:T})}{q(x_{1:T}|x_0)}\right]\\ & \ge {\mathbb{E}}_{q(x_{1:T}|x_0)}[\ln \frac{p(x_{0:T})}{q(x_{1:T}|x_0)}]\text{原始的ELBO}\\ & \cdots \cdots \\ & \mathrm{此}\mathrm{处}\mathrm{省}\mathrm{略}\mathrm{若}\mathrm{干}\mathrm{推}\mathrm{导}\mathrm{过}\mathrm{程}\\ & \cdots \cdots \\ & =\begin{array}{rl}\underset{\text{reconstruction term}}{\underbrace{{\mathbb{E}}_{q(x_1|x_0)}[\ln p_{\theta }(x_0|x_1)]}}& -\underset{\text{prior matching term}}{\underbrace{{\mathbb{E}}_{q(x_{T-1}|x_0)}[D_{\text{KL}}(q(x_T|x_{T-1})||p(x_T))]}}\\ & -\sum _{t=1}^{T-1}\underset{\text{consistency term}}{\underbrace{{\mathbb{E}}_{q(x_{t-1},x_{t+1}|x_0)}[D_{\text{KL}}(q(x_t|x_{t-1})||p_{\theta }(x_t|x_{t+1}))]}}\end{array}\end{array}\end{array}\end{array}$$

最终得到的 ELBO 由如下 3 项构成：

• ${\mathbb{E}}_{q(x_1|x_0)}[\ln p_{\theta }(x_0|x_1)]$ ：重建项，其含义同 AEs 中的重建项，表示了给定一步扩散过程的情况下，模型重建出原始输入 $x_0$ 的能力。

• ${\mathbb{E}}_{q(x_{T-1}|x_0)}[D_{\text{KL}}(q(x_T|x_{T-1})||p(x_T))]$ ：先验匹配项，其含义同 AEs 中的先验匹配项，表示了前向过程 $q$ 得出的 $x_T$ 分布与其先验分布 $p(x_T)$ 的匹配程度。但是，由于这一项不含可学习的参数，再加上当 $T$ 足够大时，$p(x_T)=\mathcal{N}(x_T;0,I)$，这一项自然为0，所以并不需要对其进行优化。

  因为当 $T$ 足够大时，${\alpha }_T\to 0$，所以无论 $x_{T-1}$ 取值为何，$q(x_T|x_{T-1})=\mathcal{N}(x_T;\sqrt{{\alpha }_T}{x}_{T-1},(1-{\alpha }_T)I)$ 都趋向于 $q(x_T|x_{T-1})=\mathcal{N}(x_T;0,I)$

• ${\mathbb{E}}_{q(x_{t-1},x_{t+1}|x_0)}[D_{\text{KL}}(q(x_t|x_{t-1})||p_{\theta }(x_t|x_{t+1}))]$：一致项，使得前向过程由 $x_{t-1}$ 生成的 $x_t$ 和逆向过程由 $x_{t+1}$ 生成的 $x_t$ 的尽可能相似。

  

  Figure 2: Depiction of consistency term.

如果对 ${\mathbb{E}}_{q(x_1|x_0)}$ 这种形式的期望的实际含义感到困惑，那么就先看看 AEs 中的相关解释吧。实际上，${\mathbb{E}}_{x_1\sim q(x_1\mid x_0)}$ 可以通过随机采样来模拟。

因为最终 ELBO 中待优化的项都是期望的形式，所以可以通过 MCMC 近似求解。但是，如果直接对 (5) 中的式子进行优化，可能会导致困难。因为其中的一致项需要同时对两个随机变量 $x_{t-1},x_{t+1}$ 进行采样，这会产生更大的方差，导致优化过程不稳定，不容易收敛。

Improved ELBO

由于 VDM 的马尔可夫特性，有 $q(x_t|x_{t-1})=q(x_t|x_{t-1},x_0)$，再通过贝叶斯定理，有：

$$\begin{array}{}\text{(6)}& \begin{array}{rl}q(x_t\mid x_{t-1},x_0)& =\frac{q(x_t,x_{t-1},x_0)}{q(x_{t-1},x_0)}\\ & =\frac{q(x_{t-1}\mid x_t,x_0)\cdot q(x_t,x_0)}{q(x_{t-1},x_0)}\\ & =\frac{q(x_{t-1}\mid x_t,x_0)\cdot q(x_t\mid x_0)}{q(x_{t-1}\mid x_0)}\end{array}\end{array}$$

将（6）式代入 ELBO 的推导，可得：

$$\begin{array}{}\text{(7)}& \begin{array}{r}\begin{array}{rl}\ln p(x)& \ge {\mathbb{E}}_{q(x_{1:T}|x_0)}[\ln \frac{p(x_{0:T})}{q(x_{1:T}|x_0)}]\\ & =\begin{array}{rl}\underset{\text{reconstruction term}}{\underbrace{{\mathbb{E}}_{q(x_1|x_0)}[\ln p_{\theta }(x_0|x_1)]}}& -\underset{\text{prior matching term}}{\underbrace{D_{\text{KL}}(q(x_T|x_0)\mid p(x_T))}}\\ & -\sum _{t=2}^T\underset{\text{denoising matching term}}{\underbrace{{\mathbb{E}}_{q(x_t|x_0)}[D_{\text{KL}}(q(x_{t-1}|x_t,x_0)\mid p_{\theta }(x_{t-1}|x_t))]}}\end{array}\end{array}\end{array}\end{array}$$

expand to see detailed derivation

可以不会推导，但至少要能看懂吧

$$\begin{gathered} \begin{array}{r}\begin{array}{rl}\ln p(x)& \ge {\mathbb{E}}_{q(x_{1:T}|x_0)}[\ln \frac{p(x_{0:T})}{q(x_{1:T}|x_0)}]\\ & ={\mathbb{E}}_{q(x_{1:T}|x_0)}[\ln \frac{p(x_T)\prod _{t=1}^T{p}_{\theta }(x_{t-1}|x_t)}{\prod _{t=1}^{T}q(x_t|x_{t-1})}]\\ & ={\mathbb{E}}_{q(x_{1:T}|x_0)}[\ln \frac{p(x_T)p_{\theta }(x_0|x_1)\prod _{t=2}^T{p}_{\theta }(x_{t-1}|x_t)}{q(x_1|x_0)\prod _{t=2}^{T}q(x_t|x_{t-1})}]\\ & ={\mathbb{E}}_{q(x_{1:T}|x_0)}[\ln \frac{p(x_T)p_{\theta }(x_0|x_1)\prod _{t=2}^T{p}_{\theta }(x_{t-1}|x_t)}{q(x_1|x_0)\prod _{t=2}^{T}q(x_t|x_{t-1},x_0)}]\\ & ={\mathbb{E}}_{q(x_{1:T}|x_0)}[\ln \frac{p_{\theta }(x_T)p_{\theta }(x_0|x_1)}{q(x_1|x_0)}+\ln \prod _{t=2}^T\frac{p_{\theta }(x_{t-1}|x_t)}{q(x_t|x_{t-1},x_0)}]\\ & ={\mathbb{E}}_{q(x_{1:T}|x_0)}[\ln \frac{p(x_T)p_{\theta }(x_0|x_1)}{q(x_1|x_0)}+\ln \prod _{t=2}^T\frac{p_{\theta }(x_{t-1}|x_t)}{\frac{p(x_{t-1}|x_t,x_0)q(x_t|x_0)}{q(x_{t-1}|x_0)}}]\mathrm{使}\mathrm{用}(6)\mathrm{进}\mathrm{行}\mathrm{替}\mathrm{换}\\ & ={\mathbb{E}}_{q(x_{1:T}|x_0)}[\ln \frac{p(x_T)p_{\theta }(x_0|x_1)}{q(x_1|x_0)}+\ln \prod _{t=2}^T\frac{p_{\theta }(x_{t-1}|x_t)}{\frac{p(x_{t-1}|x_t,x_0)\cancel{q(x_t|x_0)}}{\cancel{q(x_{t-1}|x_0)}}}]\mathrm{相}\mathrm{邻}\mathrm{项}\mathrm{可}\mathrm{以}\mathrm{消}\mathrm{去}\\ & ={\mathbb{E}}_{q(x_{1:T}|x_0)}[\ln \frac{p(x_T)p_{\theta }(x_0|x_1)}{\cancel{q(x_1|x_0)}}+\ln \frac{\cancel{q(x_1|x_0)}}{q(x_T|x_0)}+\ln \prod _{t=2}^T\frac{p_{\theta }(x_{t-1}|x_t)}{q(x_{t-1}|x_t,x_0)}]\\ & ={\mathbb{E}}_{q(x_{1:T}|x_0)}[\ln \frac{p(x_T)p_{\theta }(x_0|x_1)}{q(x_T|x_0)}+\sum _{t=2}^T\ln \frac{p_{\theta }(x_{t-1}|x_t)}{q(x_{t-1}|x_t,x_0)}]\\ & =\begin{array}{r}{\mathbb{E}}_{q(x_{1:T}|x_0)}[\ln p_{\theta }(x_0|x_1)] \\ +{\mathbb{E}}_{q(x_{1:T}|x_0)}[\ln \frac{p(x_T)}{q(x_T|x_0)}] \\ +\sum _{t=2}^T{\mathbb{E}}_{q(x_{1:T}|x_0)}[\ln \frac{p_{\theta }(x_{t-1}|x_t)}{q(x_{t-1}|x_t,x_0)}]\end{array}\\ & =\begin{array}{r}{\mathbb{E}}_{q(x_1|x_0)}[\ln p_{\theta }(x_0|x_1)]+{\mathbb{E}}_{q(x_T|x_0)}[\ln \frac{p(x_T)}{q(x_T|x_0)}] \\ +\sum _{t=2}^T{\mathbb{E}}_{q(x_t,x_{t-1}|x_0)}[\ln \frac{p_{\theta }(x_{t-1}|x_t)}{q(x_{t-1}|x_t,x_0)}] \\ \end{array}\\ & =\begin{array}{rl}\underset{\text{reconstruction term}}{\underbrace{{\mathbb{E}}_{q(x_1|x_0)}[\ln p_{\theta }(x_0|x_1)]}}& -\underset{\text{prior matching term}}{\underbrace{D_{\text{KL}}(q(x_T|x_0)||p(x_T))}}\\ & -\sum _{t=2}^T\underset{\text{denoising matching term}}{\underbrace{{\mathbb{E}}_{q(x_t|x_0)}[D_{\text{KL}}(q(x_{t-1}|x_t,x_0)||p_{\theta }(x_{t-1}|x_t))]}}\end{array}\end{array}\end{array} \end{gathered}$$

其中值得注意的是倒数第二步，实际上用到了如下性质：

$${\mathbb{E}}_{p(x_{1:n})}f(x_i)={\int }_{x_i}f(x_i)p(x_{1:n})\mathrm{d}{x}_i={\int }_{x_i}f(x_i)p(x_i)\mathrm{d}{x}_i={\mathbb{E}}_{p(x_i)}f(x_i)$$

最终得到的 ELBO 由如下 3 项构成：

• ${\mathbb{E}}_{q(x_1|x_0)}[\ln p_{\theta }(x_0|x_1)]$ ：和 (5) 相比没有变化。

• $D_{\text{KL}}(q(x_T|x_0)\mid p(x_T))$：和 (5) 相比在形式上略有区别，对于前向过程 $q$ 得到的 $x_T$，此处是由 $x_0$ 直接得到，而在 ${\mathbb{E}}_{q(x_{T-1}|x_0)}[D_{\text{KL}}(q(x_T|x_{T-1})||p(x_T))]$ 中，是先由 $x_0$ 得到 $x_{T-1}$，再得到 $x_T$。但含义相同。

• 最后一项中，需要采样的变量只剩下 $x_t$ 一个了，其实际含义是使得模型建模的 $p_{\theta }(x_{t-1}|x_t)$ 与真实分布 $q(x_{t-1}|x_t,x_0)$ 尽可能接近。

虽然 $q$ 表示的是正向过程，而用 $q(x_{t-1}|x_t,x_0)$ 来表示逆向过程，表示的是直接由正向过程计算得到的逆向过程，即逆向过程的真实分布。

而条件项 $x_0$ 的加入也很符合直觉：作为 gt，其降噪步骤必然与原始输入 $x_0$ 相关。并且，在 (4) 式中尝试给出逆向过程的表达式时，也发现其依赖于 $p(x_0)$。

接下来就是代入计算，第二项不含可学习的参数，可以直接忽略。

Denoising matching term

首先来表达确定的 $q(x_{t-1}|x_t,x_0)$。由贝叶斯定理，我们可以将其写成如下形式：

$$\begin{array}{}\text{(8)}& q(x_{t-1}|x_t,x_0)=\frac{q(x_t|x_{t-1},x_0)\cdot q(x_{t-1}|x_0)}{q(x_t|x_0)}\end{array}$$

由模型的马尔可夫性质，我们知道 $q(x_t|x_{t-1},x_0)=q(x_t|x_{t-1})=\mathcal{N}(x_t;\sqrt{{\alpha }_t}{x}_{t-1},(1-{\alpha }_t)I)$。而 $q(x_t|x_0),q(x_{t-1}|x_0)$ 呢？到目前为止，我们只知道能够通过迭代求出它们的值，但事实上，同样可以显式给出它们的表达式：

$$\begin{array}{}\text{(9)}& \begin{array}{r}\begin{array}{rl}{x}_t& =\sqrt{\prod _{i=1}^t{\alpha }_i}{x}_0+\sqrt{1-\prod _{i=1}^t{\alpha }_i}ϵ\\ & =\sqrt{{\overline{\alpha }}_t}{x}_0+\sqrt{1-{\overline{\alpha }}_t}ϵ,\overline{\alpha }=\prod _{i=1}^t{\alpha }_i,ϵ\sim \mathcal{N}(0,\mathit{\text{I}})\\ & \sim \mathcal{N}(\sqrt{{\overline{\alpha }}_t}{x}_0,(1-{\overline{\alpha }}_t)\mathit{\text{I}})\end{array}\end{array}\end{array}$$

expand to see detailed derivation

简单的展开

$$\begin{array}{r}\begin{array}{rl}{x}_t& =\sqrt{{\alpha }_t}{x}_{t-1}+\sqrt{1-{\alpha }_t}{ϵ}_t\\ & =\sqrt{{\alpha }_t}(\sqrt{{\alpha }_{t-1}}{x}_{t-2}+\sqrt{1-{\alpha }_{t-1}}{ϵ}_{t-1})+\sqrt{1-{\alpha }_t}{ϵ}_t\\ & =\sqrt{{\alpha }_t{\alpha }_{t-1}}{x}_{t-2}+\underset{\text{两个相互独立的0均值的高斯分布相加}}{\underbrace{\sqrt{{\alpha }_t-{\alpha }_t{\alpha }_{t-1}}{ϵ}_{t-1}+\sqrt{1-{\alpha }_t}{ϵ}_t}}\\ & =\sqrt{{\alpha }_t{\alpha }_{t-1}}{x}_{t-2}+\underset{\text{两个方差相加，用一个新的高斯分布代替}}{\underbrace{\sqrt{{\sqrt{{\alpha }_t-{\alpha }_t{\alpha }_{t-1}}}^2+{\sqrt{1-{\alpha }_t}}^2}ϵ}}\\ & =\sqrt{{\alpha }_t{\alpha }_{t-1}}{x}_{t-2}+\sqrt{1-{\alpha }_t{\alpha }_{t-1}}ϵ\\ & =...\\ & =\sqrt{\prod _{i=1}^t{\alpha }_i}{x}_0+\sqrt{1-\prod _{i=1}^t{\alpha }_i}ϵ\\ & =\sqrt{{\overline{\alpha }}_t}{x}_0+\sqrt{1-{\overline{\alpha }}_t}ϵ,\overline{\alpha }=\prod _{i=1}^t{\alpha }_i,ϵ\sim \mathcal{N}(0,\mathit{\text{I}})\\ & \sim \mathcal{N}(\sqrt{{\overline{\alpha }}_t}{x}_0,(1-{\overline{\alpha }}_t)\mathit{\text{I}})\end{array}\end{array}$$

然后，我们就可以将这三项代入 $q(x_t|x_{t-1},x_0)$ 中进行化简：

$$\begin{array}{}\text{(10)}& \begin{array}{r}\begin{array}{rl}q(x_{t-1}|x_t,x_0)& =\frac{q(x_t|x_{t-1},x_0)q(x_{t-1}|x_0)}{q(x_t|x_0)}\\ & =\frac{\mathcal{N}(x_t;\sqrt{{\alpha }_t}{x}_{t-1},(1-{\alpha }_t)\mathit{\text{I}})\mathcal{N}(x_{t-1};\sqrt{{\overline{\alpha }}_{t-1}}{x}_0,(1-{\overline{\alpha }}_{t-1})\mathit{\text{I}})}{\mathcal{N}(x_t;\sqrt{{\overline{\alpha }}_t}{x}_0,(1-{\overline{\alpha }}_t)\mathit{\text{I}})}\\ & \propto \mathcal{N}(x_{t-1};\underset{{\mu }_q(x_t,x_0)}{\underbrace{\frac{\sqrt{{\alpha }_t}(1-{\overline{\alpha }}_{t-1})x_t+\sqrt{{\overline{\alpha }}_{t-1}}(1-{\alpha }_t)x_0}{1-{\overline{\alpha }}_t}}},\underset{{\mathrm{\Sigma }}_q(t)}{\underbrace{\frac{(1-{\alpha }_t)(1-{\overline{\alpha }}_{t-1})}{1-{\overline{\alpha }}_t}\mathit{\text{I}}}})\end{array}\end{array}\end{array}$$

expand to see detailed derivation

$$\begin{array}{r}\begin{array}{rl}q(x_{t-1}|x_t,x_0)& =\frac{q(x_t|x_{t-1},x_0)q(x_{t-1}|x_0)}{q(x_t|x_0)}\\ & =\frac{\mathcal{N}(x_t;\sqrt{{\alpha }_t}{x}_{t-1},(1-{\alpha }_t)\mathit{\text{I}})\mathcal{N}(x_{t-1};\sqrt{{\overline{\alpha }}_{t-1}}{x}_0,(1-{\overline{\alpha }}_{t-1})\mathit{\text{I}})}{\mathcal{N}(x_t;\sqrt{{\overline{\alpha }}_t}{x}_0,(1-{\overline{\alpha }}_t)\mathit{\text{I}})}\\ & \propto \text{exp}\{-[\frac{(x_t-\sqrt{{\alpha }_t}{x}_{t-1}{)}^2}{2(1-{\alpha }_t)}+\frac{(x_{t-1}-\sqrt{{\overline{\alpha }}_{t-1}}{x}_0{)}^2}{2(1-{\overline{\alpha }}_{t-1})}-\frac{(x_t-\sqrt{{\overline{\alpha }}_t}{x}_0{)}^2}{2(1-{\overline{\alpha }}_t)}]\}\\ & =\text{exp}\{-\frac{1}{2}[\frac{(x_t-\sqrt{{\alpha }_t}{x}_{t-1}{)}^2}{1-{\alpha }_t}+\frac{(x_{t-1}-\sqrt{{\overline{\alpha }}_{t-1}}{x}_0{)}^2}{1-{\overline{\alpha }}_{t-1}}-\frac{(x_t-\sqrt{{\overline{\alpha }}_t}{x}_0{)}^2}{1-{\overline{\alpha }}_t}]\}\\ & =\text{exp}\{-\frac{1}{2}[\frac{(-2\sqrt{{\alpha }_t}{x}_t{x}_{t-1}+{\alpha }_t{x}_{t-1}^2)}{1-{\alpha }_t}+\frac{(x_{t-1}^2-2\sqrt{{\overline{\alpha }}_{t-1}}{x}_{t-1}{x}_0)}{1-{\overline{\alpha }}_{t-1}}+C(x_t,x_0)]\}\\ & \propto \text{exp}\{-\frac{1}{2}[-\frac{2\sqrt{{\alpha }_t}{x}_t{x}_{t-1}}{1-{\alpha }_t}+\frac{{\alpha }_t{x}_{t-1}^2}{1-{\alpha }_t}+\frac{x_{t-1}^2}{1-{\overline{\alpha }}_{t-1}}-\frac{2\sqrt{{\overline{\alpha }}_{t-1}}{x}_{t-1}{x}_0}{1-{\overline{\alpha }}_{t-1}}]\}\\ & =\text{exp}\{-\frac{1}{2}[(\frac{{\alpha }_t}{1-{\alpha }_t}+\frac{1}{1-{\overline{\alpha }}_{t-1}})x_{t-1}^2-2(\frac{\sqrt{{\alpha }_t}{x}_t}{1-{\alpha }_t}+\frac{\sqrt{{\overline{\alpha }}_{t-1}}{x}_0}{1-{\overline{\alpha }}_{t-1}})x_{t-1}]\}\\ & =\text{exp}\{-\frac{1}{2}[\frac{{\alpha }_t(1-{\overline{\alpha }}_{t-1})+1-{\alpha }_t}{(1-{\alpha }_t)(1-{\overline{\alpha }}_{t-1})}{x}_{t-1}^2-2(\frac{\sqrt{{\alpha }_t}{x}_t}{1-{\alpha }_t}+\frac{\sqrt{{\overline{\alpha }}_{t-1}}{x}_0}{1-{\overline{\alpha }}_{t-1}})x_{t-1}]\}\\ & =\text{exp}\{-\frac{1}{2}[\frac{{\alpha }_t-{\overline{\alpha }}_t+1-{\alpha }_t}{(1-{\alpha }_t)(1-{\overline{\alpha }}_{t-1})}{x}_{t-1}^2-2(\frac{\sqrt{{\alpha }_t}{x}_t}{1-{\alpha }_t}+\frac{\sqrt{{\overline{\alpha }}_{t-1}}{x}_0}{1-{\overline{\alpha }}_{t-1}})x_{t-1}]\}\\ & =\text{exp}\{-\frac{1}{2}[\frac{1-{\overline{\alpha }}_t}{(1-{\alpha }_t)(1-{\overline{\alpha }}_{t-1})}{x}_{t-1}^2-2(\frac{\sqrt{{\alpha }_t}{x}_t}{1-{\alpha }_t}+\frac{\sqrt{{\overline{\alpha }}_{t-1}}{x}_0}{1-{\overline{\alpha }}_{t-1}})x_{t-1}]\}\\ & =\text{exp}\{-\frac{1}{2}\left(\frac{1-{\overline{\alpha }}_t}{(1-{\alpha }_t)(1-{\overline{\alpha }}_{t-1})}\right)[x_{t-1}^2-2\frac{(\frac{\sqrt{{\alpha }_t}{x}_t}{1-{\alpha }_t}+\frac{\sqrt{{\overline{\alpha }}_{t-1}}{x}_0}{1-{\overline{\alpha }}_{t-1}})}{\frac{1-{\overline{\alpha }}_t}{(1-{\alpha }_t)(1-{\overline{\alpha }}_{t-1})}}{x}_{t-1}]\}\\ & =\text{exp}\{-\frac{1}{2}\left(\frac{1-{\overline{\alpha }}_t}{(1-{\alpha }_t)(1-{\overline{\alpha }}_{t-1})}\right)[x_{t-1}^2-2\frac{(\frac{\sqrt{{\alpha }_t}{x}_t}{1-{\alpha }_t}+\frac{\sqrt{{\overline{\alpha }}_{t-1}}{x}_0}{1-{\overline{\alpha }}_{t-1}})(1-{\alpha }_t)(1-{\overline{\alpha }}_{t-1})}{1-{\overline{\alpha }}_t}{x}_{t-1}]\}\\ & =\text{exp}\{-\frac{1}{2}\left(\frac{1}{\frac{(1-{\alpha }_t)(1-{\overline{\alpha }}_{t-1})}{1-{\overline{\alpha }}_t}}\right)[x_{t-1}^2-2\frac{\sqrt{{\alpha }_t}(1-{\overline{\alpha }}_{t-1})x_t+\sqrt{{\overline{\alpha }}_{t-1}}(1-{\alpha }_t)x_0}{1-{\overline{\alpha }}_t}{x}_{t-1}]\}\\ & \propto \mathcal{N}(x_{t-1};\underset{{\mu }_q(x_t,x_0)}{\underbrace{\frac{\sqrt{{\alpha }_t}(1-{\overline{\alpha }}_{t-1})x_t+\sqrt{{\overline{\alpha }}_{t-1}}(1-{\alpha }_t)x_0}{1-{\overline{\alpha }}_t}}},\underset{{\mathrm{\Sigma }}_q(t)}{\underbrace{\frac{(1-{\alpha }_t)(1-{\overline{\alpha }}_{t-1})}{1-{\overline{\alpha }}_t}\mathit{\text{I}}}})\end{array}\end{array}$$

由此，我们发现由 $q(x_{t-1}|x_t,x_0)$ 得到的 $x_{t-1}$ 其实服从于 $\mathcal{N}({\mu }_q(x_t,x_0),{\mathrm{\Sigma }}_q(t))$。而 KL 散度中的另一项呢？是模型决定的 $p_{\theta }(x_t|x_{t-1})$。要使得 $p_{\theta }(x_t|x_{t-1})$ 与 $q(x_{t-1}|x_t,x_0)$ 尽可能接近，索性也让其是一个高斯分布。

• 对于方差，由于 ${\mathrm{\Sigma }}_q$ 只和时间步 $t$ 相关，逆向过程的模型也可以获取到该值，所以索性令 $p_{\theta }$ 的方差也是 ${\mathrm{\Sigma }}_q$；
• 对于均值，就不能这么干了，因为 ${\mu }_q$ 与 $x_0$ 相关，逆向过程的模型无法获取到该值，因此必须通过参数化求解，不妨设当前的均值与 $t$ 和 $x_t$ 相关。

综上所述，我们约定了 $p_{\theta }(x_{t-1}|x_t)\sim \mathcal{N}(x_t;{\mu }_{\theta }(x_t,t),{\mathrm{\Sigma }}_q(t))$，而两个高斯分布的 KL 散度又是有公式的：

$$\begin{array}{}\text{(11)}& D_{\text{KL}}(\mathcal{N}(x;{\mu }_x,{\mathrm{\Sigma }}_x)||\mathcal{N}(y;{\mu }_y,{\mathrm{\Sigma }}_y))=\frac{1}{2}[\log \frac{|{\mathrm{\Sigma }}_y|}{|{\mathrm{\Sigma }}_x|}-d+\text{tr}({\mathrm{\Sigma }}_y^{-1}{\mathrm{\Sigma }}_x)+({\mu }_y-{\mu }_x{)}^T{\mathrm{\Sigma }}_y^{-1}({\mu }_y-{\mu }_x)]\end{array}$$

因此，可以得出真实分布 $q(x_{t-1}|x_t,x_0)$ 和参数化学习分布 $p_{\theta }(x_{t-1}|x_t)$ 的 KL 散度为：

$$\begin{array}{}\text{(12)}& \begin{array}{r}\begin{array}{rl}& D_{\text{KL}}(q(x_{t-1}|x_t,x_0)||p_{\theta }(x_{t-1}|x_t))\\ & =D_{\text{KL}}(\mathcal{N}(x_{t-1};{\mu }_q,{\mathrm{\Sigma }}_q(t))||\mathcal{N}(x_{t-1};{\mu }_{\theta },{\mathrm{\Sigma }}_q(t)))\\ & =\frac{1}{2}[\log \frac{|{\mathrm{\Sigma }}_q(t)|}{|{\mathrm{\Sigma }}_q(t)|}-d+\text{tr}({\mathrm{\Sigma }}_q(t{)}^{-1}{\mathrm{\Sigma }}_q(t))+({\mu }_{\theta }-{\mu }_q{)}^T{\mathrm{\Sigma }}_q(t{)}^{-1}({\mu }_{\theta }-{\mu }_q)]\\ & =\frac{1}{2}[\log 1-d+d+({\mu }_{\theta }-{\mu }_q{)}^T{\mathrm{\Sigma }}_q(t{)}^{-1}({\mu }_{\theta }-{\mu }_q)]\\ & =\frac{1}{2}[({\mu }_{\theta }-{\mu }_q{)}^T{\mathrm{\Sigma }}_q(t{)}^{-1}({\mu }_{\theta }-{\mu }_q)]\\ & =\frac{1}{2}[({\mu }_{\theta }-{\mu }_q{)}^T{({\sigma }_q^2(t)\mathbf{\text{I}})}^{-1}({\mu }_{\theta }-{\mu }_q)]\\ & =\frac{1}{2{\sigma }_q^2(t)}\left[{\Vert {\mu }_{\theta }-{\mu }_q\Vert }_2^2\right]\end{array}\end{array}\end{array}$$

极大化 ELBO 函数，等价于极小化 (12)，等价于使得每个时间步，模型的 ${\mu }_{\theta }(x_t,t)$ 与 真实分布的 ${\mu }_q(x_t,x_0)$ 尽可能接近。于是，我们又可以索性令 ${\mu }_{\theta }(x_t,t)$ 与 ${\mu }_q$ 具有相似的形式：

$$\begin{array}{}\text{(13)}& {\mu }_{\theta }(x_t,t)=\frac{\sqrt{{\alpha }_t}(1-{\overline{\alpha }}_{t-1})x_t+\sqrt{{\overline{\alpha }}_{t-1}}(1-{\alpha }_t){\hat{x}}_{\theta }(x_t,t)}{1-{\overline{\alpha }}_t}\end{array}$$

换言之，模型只需要预测其中的 ${\hat{x}}_{\theta }(x_t,t)$。于是乎，我们可以进一步简化 (12) 中的极小化目标：

$$\begin{array}{}\text{(14)}& \begin{array}{r}\begin{array}{rl}& {\arg max}_{\theta }[D_{\text{KL}}(q(x_{t-1}|x_t,x_0)||p_{\theta }(x_{t-1}|x_t))]\\ =& {\arg min}_{\theta }\left[\frac{1}{2{\sigma }_q^2(t)}\left[{\Vert {\mu }_{\theta }-{\mu }_q\Vert }_2^2\right]\right]\\ \iff & {\arg min}_{\theta }\left[{\Vert {\mu }_{\theta }-{\mu }_q\Vert }_2^2\right]\\ =& {\arg min}_{\theta }\left[\frac{\sqrt{{\overline{\alpha }}_{t-1}}(1-{\alpha }_t)}{1-{\overline{\alpha }}_t}{\Vert ({\hat{x}}_{\theta }(x_t,t)-x_0)\Vert }_2^2\right]\\ \iff & {\arg min}_{\theta }\left[{\Vert ({\hat{x}}_{\theta }(x_t,t)-x_0)\Vert }_2^2\right]\end{array}\end{array}\end{array}$$

Reconstruction term

相对 denoising matching 项来说，这一项并没有涉及很多的求和项，所以对于逆向过程模型的假设都是以 denoising matching 项分析中的“索性令”为准。

多元高斯分布的概率密度函数为：

$$\begin{array}{}\text{(15)}& {\displaystyle f_{\mathbf{x}}(x_1,\dots ,x_k)=\frac{1}{\sqrt{(2\pi {)}^k|\mathbf{\Sigma }|}}{\mathrm{e}}^{-\frac{1}{2}(\mathbf{x}-\mathit{\mu }{)}^{\mathrm{T}}{\mathbf{\Sigma }}^{-1}(\mathbf{x}-\mathit{\mu })}}\end{array}$$

据此化简 reconstruction term：

$$\begin{array}{}\text{(16)}& \begin{array}{r}\begin{array}{rl}& {\arg max}_{\theta }{\mathbb{E}}_{q(x_1|x_0)}\ln p_{\theta }(x_0|x_1)\\ =& {\arg max}_{\theta }{\mathbb{E}}_{q(x_1|x_0)}\ln (\frac{1}{\sqrt{(2\pi {)}^d|{\mathrm{\Sigma }}_q(1)|}}\exp \{-\frac{1}{2}(x_0-{\mu }_{\theta }(x_1,1){)}^T{\mathrm{\Sigma }}_q(1{)}^{-1}(x_0-{\mu }_{\theta }(x_1,1))\})\\ \iff & {\arg min}_{\theta }{\mathbb{E}}_{q(x_1|x_0)}{\Vert x_0-{\mu }_{\theta }(x_1,1)\Vert }_2^2\end{array}\end{array}\end{array}$$

又因为 ${\mu }_{\theta }(x_1,1)$ 需要用到 ${\overline{\alpha }}_0$，这个值并没有定义（事实上在 denoising matching 项中，$t$ 的下界也是 2），这里我们不妨另其为 $1$，则可以进一步将优化目标写作：

$$\begin{array}{}\text{(16)}& {\arg min}_{\theta }{\mathbb{E}}_{q(x_1|x_0)}{\Vert x_0-{\hat{x}}_{\theta }(x_1,1)\Vert }_2^2\end{array}$$

为什么这么写，接下来就会明白了

Final Loss

结合以上两项的结果，我们可以得出最终的优化目标：

$$\begin{array}{}\text{(17)}& \begin{array}{r}\begin{array}{rl}& {\arg max}_{\theta }\text{ELBO}\\ & \iff {\arg max}_{\theta }[{\mathbb{E}}_{q(x_1|x_0)}[\ln p_{\theta }(x_0|x_1)]-\sum _{t=2}^T{\mathbb{E}}_{q(x_t|x_0)}[D_{\text{KL}}(q(x_{t-1}|x_t,x_0)||p_{\theta }(x_{t-1}|x_t))]]\\ & \iff {\arg min}_{\theta }\left[{\mathbb{E}}_{q(x_1|x_0)}\left[{\Vert x_0-{\hat{x}}_{\theta }(x_1,1)\Vert }_2^2\right]\right]+\left[\sum _{t=2}^T{\mathbb{E}}_{q(x_t|x_0)}\left[{\Vert ({\hat{x}}_{\theta }(x_t,t)-x_0)\Vert }_2^2\right]\right]\\ & \iff {\arg min}_{\theta }\sum _{t=1}^T{\mathbb{E}}_{q(x_t|x_0)}\left[{\Vert ({\hat{x}}_{\theta }(x_t,t)-x_0)\Vert }_2^2\right]\end{array}\end{array}\end{array}$$

从目标函数中可以发现，模型在每个时间步 $t$ 都在预测原始输入 $x_0$，而推理过程却是使用 ${\hat{x}}_{\theta }(x_t,t)$ 来计算 ${\mu }_{\theta }$，从而结合 ${\mathrm{\Sigma }}_q(t)$ 计算出 $p_{\theta }(x_{t-1}|x_t)$，最终随机采样得到 $x_{t-1}$。通过 $T$ 步采样得出最终的输出。直觉上讲，每一步预测的 ${\hat{x}}_{\theta }$ 目标按道理是不同的。

After reading

经过如此冗长的推导，我们不妨来回顾一下整个过程：

1. 生成过程是基于一个 MHVAE；
2. 因为前向过程确定，我们实际上要学习的是从 $p(x_T)$ 这个先验高斯分布，采样还原出 $p(x_0)$ 的逆向过程 $q(x_t\mid x_{t+1})$；
3. 采用 MLE 进行学习，可观测的生成样本只有 $x_0$；
4. 经过一系列推导，得出目标函数中的若干项，其中高斯分布极大简化了推导过程；
5. 因为目标是最小化损失函数，因此我们可以令 $q_{\theta }$ 具有和已知概率密度函数相似的结构，而将无法直接获取的部分留待网络学习；