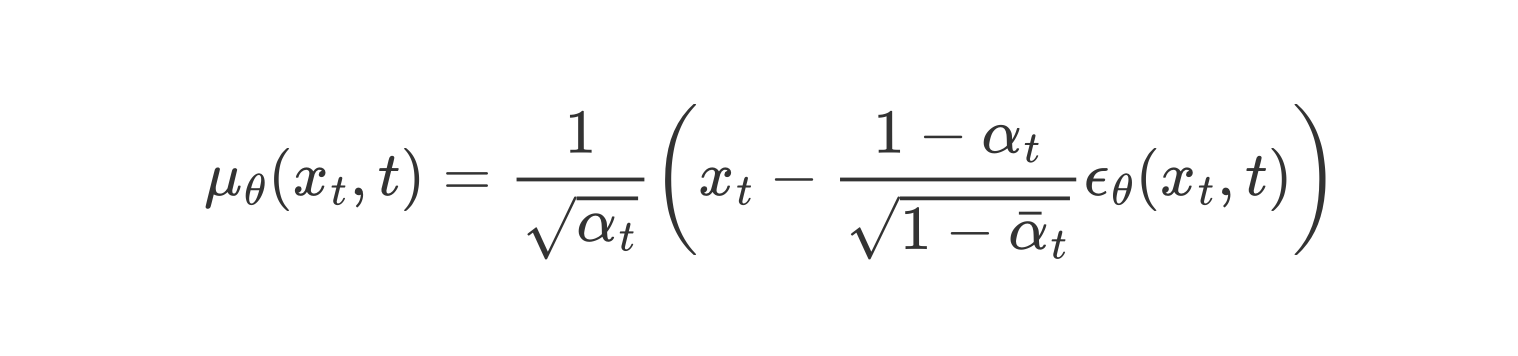DMs[2] DDPM

• Paper
• Github Repo

Overview

在 DMs[1] DPM 中，模型需要在每个时间步预测 ${\hat{x}}_{\theta }(x_t,t)$ 来逼近 $x_0$，并以此来计算出 $t$ 时间步逆向过程的均值、方差，从而采样得到 $x_{t-1}$。虽然整个过程循序渐进地经过了 $T$ 步，以得到最终的输出 $x_0$，但模型预测的内容却不是随时间变化的。这会导致模型训练效果较差。那么，有没有对于目标函数的另一种推导，能够让模型预测的内容也与当前时间步相关呢？

这就要提到 DDPM(Denoising diffusion probabilistic model)，它基于与 DPM 完全一致的数学模型，但对目标函数采用了不同的推导方法，对参数化模型预测的内容做了调整。

Method

Derivation

expand to see ELBO

$$\begin{array}{r}\begin{array}{rl}\ln p(x_0)& \ge {\mathbb{E}}_{q(x_{1:T}|x_0)}[\ln \frac{p(x_{0:T})}{q(x_{1:T}|x_0)}]\\ & =\begin{array}{rl}\underset{\text{reconstruction term}}{\underbrace{{\mathbb{E}}_{q(x_1|x_0)}[\ln p_{\theta }(x_0|x_1)]}}& -\underset{\text{prior matching term}}{\underbrace{D_{\text{KL}}(q(x_T|x_0)\mid p(x_T))}}\\ & -\sum _{t=2}^T\underset{\text{denoising matching term}}{\underbrace{{\mathbb{E}}_{q(x_t|x_0)}[D_{\text{KL}}(q(x_{t-1}|x_t,x_0)\mid p_{\theta }(x_{t-1}|x_t))]}}\end{array}\end{array}\end{array}$$

Denoising matching term

回顾对于 DPM ELBO 中 denoising matching 项的化简结果：

$$\begin{array}{}\text{(1)}& \begin{array}{r}\begin{array}{rl}& D_{\text{KL}}(q(x_{t-1}|x_t,x_0)||p_{\theta }(x_{t-1}|x_t))=\frac{1}{2{\sigma }_q^2(t)}\left[{\Vert {\mu }_{\theta }-{\mu }_q\Vert }_2^2\right]\end{array}\end{array}\end{array}$$

其中，由真实分布给定的${\mu }_q$ 的表达式如下：

$$\begin{array}{}\text{(2)}& {\mu }_q(x_t,t)=\frac{\sqrt{{\alpha }_t}(1-{\overline{\alpha }}_{t-1})x_t+\sqrt{{\overline{\alpha }}_{t-1}}(1-{\alpha }_t)x_0}{1-{\overline{\alpha }}_t}\end{array}$$

在 DPM 中，我们直接令 ${\mu }_{\theta }$ 具有与 (2) 类似的形式：

$$\begin{array}{}\text{(3)}& {\mu }_{\theta }(x_t,t)=\frac{\sqrt{{\alpha }_t}(1-{\overline{\alpha }}_{t-1})x_t+\sqrt{{\overline{\alpha }}_{t-1}}(1-{\alpha }_t){\hat{x}}_{\theta }(x_t,t)}{1-{\overline{\alpha }}_t}\end{array}$$

但 DDPM 没有这么做，而是对 (2) 进行了进一步的改写。首先我们知道：

$$\begin{array}{}\text{(4)}& \begin{array}{rl}{x}_t(x_0,ϵ)& =\sqrt{{\alpha }_t}{x}_{t-1}+\sqrt{1-{\alpha }_t}ϵ\\ & =\sqrt{\prod _{i=1}^t{\alpha }_i}{x}_0+\sqrt{1-\prod _{i=1}^t{\alpha }_i}ϵ\\ & =\sqrt{{\overline{\alpha }}_t}{x}_0+\sqrt{1-{\overline{\alpha }}_t}ϵ,\overline{\alpha }=\prod _{i=1}^t{\alpha }_i,ϵ\sim \mathcal{N}(0,\mathit{\text{I}})\end{array}\end{array}$$

根据 (4) 式，我们知道 $x_0=\frac{x_t-\sqrt{1-{\overline{\alpha }}_t}ϵ}{\sqrt{{\overline{\alpha }}_t}}$，从而将 (2) 式中出现的 $x_0$ 替换成 $ϵ$：

$$\begin{array}{}\text{(5)}& \begin{array}{rl}{\mu }_q(x_t,t)& =\frac{\sqrt{{\alpha }_t}(1-{\overline{\alpha }}_{t-1})x_t+\sqrt{{\overline{\alpha }}_{t-1}}(1-{\alpha }_t)\cdot \frac{x_t-\sqrt{1-{\overline{\alpha }}_t}ϵ}{\sqrt{{\overline{\alpha }}_t}}}{1-{\overline{\alpha }}_t}\\ & =\frac{\sqrt{{\alpha }_t}(1-{\overline{\alpha }}_{t-1})x_t+(1-{\alpha }_t)\cdot \frac{x_t-\sqrt{1-{\overline{\alpha }}_t}ϵ}{\sqrt{{\alpha }_t}}}{1-{\overline{\alpha }}_t}\\ & =\frac{1}{\sqrt{{\alpha }_t}}(x_t-\frac{1-{\alpha }_t}{\sqrt{1-{\overline{\alpha }}_t}}ϵ)\end{array}\end{array}$$

采取与 DPM 中同样的处理思路，对于确定的参数，我们直接令 ${\mu }_{\theta }$ 与之一致。因此，我们可以将 ${\mu }_{\theta }$ 建模如下，并得到对应的 denoising matching 项：

$$\begin{array}{}\text{(6)}& {\mu }_{\theta }(x_t,t)=\frac{1}{\sqrt{{\alpha }_t}}(x_t-\frac{1-{\alpha }_t}{\sqrt{1-{\overline{\alpha }}_t}}{ϵ}_{\theta }(x_t,t))\end{array}$$$$\begin{array}{}\text{(7)}& \begin{array}{r}\begin{array}{rl}& D_{\text{KL}}(q(x_{t-1}|x_t,x_0)||p_{\theta }(x_{t-1}|x_t))\\ & =\frac{1}{2{\sigma }_q^2(t)}\left[{\Vert {\mu }_{\theta }-{\mu }_q\Vert }_2^2\right]\\ & =\frac{1}{2{\sigma }_q^2(t)}\frac{(1-{\alpha }_t{)}^2}{(1-{\overline{\alpha }}_t){\alpha }_t}\left[{\Vert ϵ-{\widehat{ϵ}}_{\theta }(x_t,t)\Vert }_2^2\right]\end{array}\end{array}\end{array}$$

这样，我们就能很清楚地看出，在 $t\to t-1$ 时，DDPM 需要模型去预测正向过程 $t-1\to t$ 时所添加的噪声 $ϵ$ ，从而实现了预测目标与时间步相关联。

Reconstruction term

最后一步 $x_1\to x_0$ 略有不同。

$$\begin{array}{}\text{(8)}& p_{\theta }({\mathbf{x}}_0|{\mathbf{x}}_1)=\prod _{i=1}^D{\int }_{{\delta }_{-}(x_0^i)}^{{\delta }_{+}(x_0^i)}\mathcal{N}(x;{\mu }_{\theta }^i({\mathbf{x}}_1,1),{\sigma }_1^2)dx\end{array}$$$$\begin{array}{}\text{(9)}& \begin{array}{r}{\delta }_{-}(x)=\{\begin{array}{ll}-\mathrm{\infty }& \text{if }x=-1\\ x-\frac{1}{255}& \text{if }x>-1\end{array}{\delta }_{+}(x)=\{\begin{array}{ll}\mathrm{\infty }& \text{if }x=1\\ x+\frac{1}{255}& \text{if }x<1\end{array}\end{array}\end{array}$$

todo

Train and Sample

基于上述推导，在原理上已经可以进行训练，但文章发现，基于如下简化版本的损失函数可以维持相近的生成质量：

$$\begin{array}{}\text{(10)}& L_{\text{simple}}(\theta ):={\mathbb{E}}_{t,x_0,ϵ}\left[{\Vert ϵ-{ϵ}_{\theta }(\sqrt{{\overline{\alpha }}_t}{x}_0+\sqrt{1-{\overline{\alpha }}_t}ϵ,t)\Vert }^2\right]\end{array}$$

相比原始形式，$L_{\text{simple}}$ 有如下变化：

• 不再区分 denoising matching 项 和 reconstruction 项；
• 将 denoising matching 项中的对 $t$ 求和替换为对 $t$ 求期望，最终通过随机采样实现；
• 相比原始的 denoising matching 项，去掉了系数；
• 根据期望中的函数参数，修改了期望的下标。

最终，得出训练算法以及推理（采样）算法如下：

Figure 1: Training Algorithm for DDPM.

Figure 2: Sampling Algorithm for DDPM.

注意到在采样过程的最后一步，模型略去了 ${\sigma }_t\mathbf{\text{z}}$ 项。模型 $p_{\theta }(x_{t-1}|x_t)$ 拟合了真实分布 $q(x_{t-1}|x_t,x_0)$，这是一个条件概率，并不能确定计算出 $x_{t-1}$，而是一个随机采样过程，这体现在 ${\sigma }_t\mathbf{\text{z}}$ 项中。然而，这只对 $t\in [2,T]$ 成立（因为这样的做法是从 denoising matching 项中推导出的）。对于 $x_1\to x_0$ 的过程，我们可以直接从前向过程入手：

$$\begin{array}{}\text{(11)}& \begin{array}{rl}{x}_1& =\sqrt{{\alpha }_1}{x}_0+\sqrt{1-{\alpha }_1}ϵ\\ x_0& =\frac{1}{\sqrt{{\alpha }_1}}(x_1-\sqrt{1-{\alpha }_1}ϵ)\\ & =\frac{1}{\sqrt{{\alpha }_1}}(x_1-\frac{1-{\alpha }_t}{\sqrt{1-{\alpha }_1}}ϵ)\end{array}\end{array}$$

我们发现 $x_0$ 的表达式刚好符合 $t\in [2,T]$ 过程的表达式，而仅仅舍去了 ${\sigma }_t\mathbf{\text{z}}$ 项。而在这篇博客中，作者指出，此时 ${\hat{x}}_0$ 刚好与 $\hat{\mu }(x_1,1)$ 相同，这也就是说，最终输出是（拟合） $q(x_{t-1}|x_t,x_0,1)$ 的期望，而不是采样值，这与 reconstruction 项相吻合。

After reading

基于 VDM 这个数学模型，其实可以推导出很多不同的目标函数形式，其核心是基于数学推导，在某一步选择抽出公式中某个无法通过数学表达的项，用参数化模型去拟合。然后，推导训练的目标函数和推理过程。

DDPM 的拟合目标具有很强的实际意义：预测每一步添加的噪声。但这不代表可以舍弃数学推导，直接猜拟合目标：就算猜到了 ${ϵ}_{\theta }(x_t,t)$，也不知道该怎么用它进行逆向过程，毕竟不是直接减去预测噪声。